IRAS Explanatory Supplement
V. Data Reduction
D. Point Source Confirmation
D.9 Conversion of Position Uncertainties to Gaussian Approximation
Table of Contents | Index | Previous Section | Next Section
Throughout the processing, the position error model was based on the non-Gaussian formalism mentioned in Section V.D.1. Because most of the point source position probability density functions evolve toward Gaussian shapes at each stage of refinement, the catalog description was designed to approximate the more familiar error eclipses of two-dimensional Gaussians, while retaining most of the accuracy of the non-Gaussian model. This involved bracketing the nominal positions on each coordinate axis with a single number to be interpreted as a confidence interval on that axis. This is a simplification of the optimal cross-scan description, which requires two numbers to define the distribution about the mean.
For sources with strongly non-Gaussian position uncertainties, there is no way to escape the fact that some aspects of the error behavior will not generally be Gaussian. An important specific example is the relation between error in sigma units and the fraction of all cases exceeding that error. Because of the decision to quote the axes of the two-dimensional contour enclosing 95% of the probability mass, the error bars given were selected to match the corresponding deviations on the axes of the random variables used in the error model. Thus the expected frequency at which the true source position lies outside of the quoted contour is 5%. The contour is not generally elliptical, however, as this is a Gaussian feature not necessarily shared by the actual distributions. The error incurred by assuming that the contours are all elliptical, on the other hand should not be extreme, and in fact this approximation played a role in mapping the two-dimensional 95% confidence into one-dimensional confidences on each axis.
The error bars were obtained as follows. For Gaussian errors,
the two-dimensional 95% confidence would correspond to a
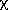 2 probability of 0.95 with two
degrees of freedom.
This implies a value of 5.99 for the
2 probability of 0.95 with two
degrees of freedom.
This implies a value of 5.99 for the
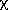 2 random
variable, so that the eclipse crosses each axis at
2.45-
2 random
variable, so that the eclipse crosses each axis at
2.45- ,
corresponding to a confidence of 98.6%. This was used for the
confidence level for both axes. On the Gaussian axis of the
error model, the interval used was
2.45-
,
corresponding to a confidence of 98.6%. This was used for the
confidence level for both axes. On the Gaussian axis of the
error model, the interval used was
2.45- y. On
the non-Gaussian axis, a lookup table was used to obtain the
98.6% confidence deviation as a function of the ratio of the
uniform half-width, Lz, to the Gaussian
y. On
the non-Gaussian axis, a lookup table was used to obtain the
98.6% confidence deviation as a function of the ratio of the
uniform half-width, Lz, to the Gaussian
 z. This table was
computed by numerical
quadrature for a grid of these ratios ranging from 0.1 to 30.
Below 0.1, the probability density was considered Gaussian,
and above 30 it was taken as purely uniform.
z. This table was
computed by numerical
quadrature for a grid of these ratios ranging from 0.1 to 30.
Below 0.1, the probability density was considered Gaussian,
and above 30 it was taken as purely uniform.
Table of Contents | Index | Previous Section | Next Section