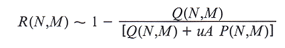IRAS Explanatory Supplement
VIII. Sky Coverage, Confusion, Completeness and Reliability
D. Point Source Catalog Reliability and Completeness
D.2 Formalism for the Determination of Completeness and Reliability
Chapter Contents | Authors | References
Table of Contents | Index | Previous Section | Next Section
D.2.a Completeness
It is necessary to estimate the fraction of real sources on the sky,
above some limiting flux density value, which is actually present in the
catalog. Let p be the probability that a genuine source in a given
flux range fails to generate an HCON. The probability
P(N,M)
that a source is detected on N HCONs out of a possible M
HCONs is given by:
(VIII.D.1)
where mCn is the binomial coefficient.
The completeness C(Nmin, M) of a
Nmin/M survey, which requires a source to have at
least Nmin
HCONs out of M possible in order to be included in the catalog, is then
given by:
(VIII.D.2)
for a survey where two HCONs are required out of a possible two HCONs,
the completeness C(2,2) is given by:
(VIII.D.3)
Seventy two percent of the sky was surveyed three times and a source
was accepted if it was seen at least twice.
For this "two-out-of-three" strategy, the completeness
C(2,3) is given by.:
(VIII.D.4)
where the first term on the right-hand side of the first equation corresponds
to having seen the source twice out of the three possible times while the
second corresponds to seeing it all three times. The completeness of the
2/3 survey is therefore a factor (1 + 2p) greater than that of a 2/2
survey. This factor is appreciable since most sources are near the
completeness limit where p approaches 1. In small areas of the sky the
completeness
will be better than suggested by Eq. (VIII.D.4) since
there were as many as 23 HCON coverages, yet only two HCONs were required
for inclusion in the catalog (see
Table VII.B.1).
(VIII.D.5)
In fact, Eq. (VIII.D.5) is only true if qA
« 1 since it does not allow for the possibility that more than one
false source is created within A during a single HCON. This is a
necessary assumption for the IRAS processing because, by its very nature,
the processing can only produce one final source per HCON from an area
A. The results obtained justify the approximation.
Let u be the density of true sources in a given region of the
sky. The probability of detecting a true source on N out of M
HCONs in a given area of the sky is uA P(N,M)
where P(N,M) is given by Eq.
(VIII.D.2); it is necessary that uA « 1. Hence the total
probability T(N,M) of finding a source, either false or
true, on N out of M HCONs in a given area of the sky is given
by:
(VIII.D.6)
where cross terms have been neglected. The reliability
R(N,M) of an N/M source is unity minus
the probability that the source is false. The probability that a given source
is false is the probability of finding a false source divided by the total
probability of finding any source. Therefore,
(VIII.D.7)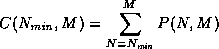
= (1 + 2p)(1 - p)2
Let q be the probability, per unit area of the sky, that a false
source is created on a single HCON coverage of the sky. Let A be
the effective area for "weeks-confirmation" (see Sections
V.D,
V.H.2), i.e. the area within which a series
of single HCONs must fall if they are to be considered as detections of
the same source. Then qA is the probability that in a single HCON
coverage a false source will be created at a given point on the sky with
the possibility of being confirmed with another false source at the same
position on a later HCON. The probability Q(N,M) that
a false source will be created in a given area N times out of M
HCONs is therefore given by
D.2.b Reliability