ISSA Explanatory Supplement
APPENDIX G
Zodiacal Dust Cloud Modeling Using IRAS Data
J. Good
G.1 Overview
A physical model for the interplanetary dust cloud was fit to the IRAS data. This model consists of spatial distributions for the dust volumetric emissivity and temperature, an inclination and line of nodes for the cloud, and a simple parameterization of the dust emissivity as a function of wavelength. The volumetric emissivity was found to vary as r-1.8 × exp[-4.97 (|z|/r)1.26] and the temperature as R-0.36, where R is the radial distance from the Sun in spherical coordinates, r is the radial distance from the Sun in cylindrical coordinates and z is the distance from the plane of symmetry of the dust. This density drop-off differs from the r-1.3 power law for the dust density deduced from Helios measurements of scattered sunlight, but the discrepancy can be explained if the albedo of the dust decreases with heliocentric distance.|
|
|
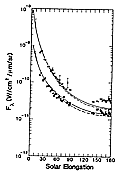
Figure G.1 ZIP data (Murdock and Price 1985)
showing zodiacal brightness in the ecliptic plane as a function of
solar elongation. The dashed curve represents the predicted flux
(scaled by a factor of 1.5)
from the zodiacal dust cloud model. larger largest |
The IRAS data are limited to solar elongation angles between 60° and 120° and consequently are not sensitive to material closer to the Sun than about 0.9 AU. However, comparison of the predicted model flux and Zodiacal Infrared Project (ZIP) data (Murdock and Price 1985) which looked to within 22° of the Sun at 10 and 20 µm shows excellent agreement in shape (Figure G.1), though there is a calibration scale discrepancy. It also implies that the r-1.8 power law is good to 0.4 AU. The inclination of the zodiacal dust cloud is 1.7° and its line of ascending nodes is at 69° ecliptic longitude, substantially different from the 3.4° and 87° deduced from the Helios measurements. However, since the Helios measurements were made between 0.3 and 1 AU and the IRAS data is primarily sensitive to material outside 0.9 AU, we attribute these differences to variation of the cloud symmetry plane with heliocentric distance.
The model presented here is based on the IRAS data as understood after the final calibration. Preliminary comparisons of IRAS data with the COBE-DIRBE data suggests that the IRAS gains and offsets require small change (§IV.D.3 and DIRBE Explanatory Supplement, 19 July 1993). Consequently, the physical parameters determined for the zodiacal dust cloud need reinterpretation. However, the purpose here is to represent accurately the variability of the infrared background and the current model does that quite well.
G.2 Data
The IRAS data provide us with an unprecedented opportunity to investigate the zodiacal dust cloud. First, the sheer volume of data makes it possible to fit for a large number of dust cloud parameters unambiguously. Furthermore, the extremely high signal-to-noise allows differentiation and exclusion of Galactic IR structure. Finally, the spectral coverage (7-140 µm in four bands) allows concurrent extraction of temperature and emissivity information.|
|
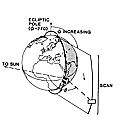
Figure G.2 The scanning geometry of the IRAS
satellite is illustrated. The scan coordinate system is defined
by the solar elongation angle  , which
remains fixed for a scan, and the inclination angle i, which
changes at a constant rate.larger largest |
The IRAS satellite was placed in a near-polar orbit of 99° inclination oriented with the orbital plane roughly normal to the Sun-Earth vector (Figure G.2). The orbit precessed through the year to maintain constant orientation to the Sun. Thus the nominal scan path during an orbit pointed directly away from the Earth and traced a line from ecliptic pole to ecliptic pole in a plane 90° away from the Sun. In practice, however, during any given half orbit (i.e., from one pole to the other) the satellite was tilted either toward or away from the Sun by varying amounts. It then swept out a cone on the sky at a constant angle from the Sun (the solar elongation angle) and with a constant azimuthal rate (3.84' s-1). The solar elongation varied by as much as ± 30° from normal but was usually within ± 10°.
The azimuth angle (referred to as the inclination angle) is arbitrarily defined to be -90° when the satellite passes the north ecliptic pole and increases in the direction of the scan. Since the descending part of the orbit occurred on the side of the Earth opposite the Earth's direction of motion (see Figure G.2), an inclination of 0° looks in the Earth's orbital plane back in the direction from which the Earth has come. Many of the coordinate angle references in this appendix (particularly on the plots) will be given in this solar elongation/inclination system.
|
|
|
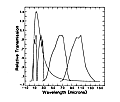
Figure G.3 The IRAS bandpasses and a 200 K
blackbody, for reference. larger largest |
The sky was observed through four wide bandpass filters, nominally centered at 12, 25, 60, and 100 µm (Figure G.3) (IRAS Explanatory Supplement 1988, §II.C). It is important for the modeling to use the exact bandpass shape, since temperature variations with heliocentric distance play an important role in the observed infrared flux. Consequently, fluxes will often be given in in-band Wm-2sr-1 and only converted to MJy sr-1 when appropriate.
Almost 6000 scans were made during the mission, about 1700 of which went from pole to pole. Of these, 200 scans were chosen which were representative of the range of solar elongations and which uniformly covered the time period of the mission. A typical scan is shown in Figure G.4.
The major portion of the flux seen at 12, 25, and 60 µm is due to the zodiacal emission we wish to model. The small local variations that are left are due to Galactic sources, which become dominant at 100 µm. It is important to note that these fluctuations are not noise (the noise is too small to show on these plots; the typical SNR is about 1,000). This proved to be a major problem in the fitting since it implied that the model should be fit to the local minima in a kind of "lower envelope" rather than the data as a whole. The method devised to handle this problem will be discussed in the section on fitting. At 100 µm there was almost no zodiacal emission on the sky that was not contaminated by a large amount of Galactic flux.
G.3 Description of Model
G.3.a Density
An adequate representation for the spatial distribution of the zodiacal dust is the most important factor in modeling of the observed infrared flux. A simple model for the variation of dust density with heliocentric distance (where the dust spirals in due to the Poynting-Robertson effect) would produce a radial distribution proportional to r-1 (Briggs 1962). Models that include mutual collisions (Trulsen and Wikan 1980; Leinert et al. 1981) and perhaps Lorentz forces (Mukai and Giese 1984) produce distributions that vary as r - k where k > 1. In this study the radial part of the density distribution is assumed to vary as r -
where is
a free parameter (r is the radial component of the distance
from the Sun in cylindrical coordinates).
The variation of density out of the plane of the ecliptic is
less clear. To fit Helios data, Leinert et
al., (1978a) used a z-dependence of exp[-2.1(|z|/r)]. Collision
models (Trulsen and Wikan 1980) indicate
that exp[-
r2] might be more appropriate. In this study
the z-dependence is assumed to be of the form
exp[-(|z|/r)
] where and are free parameters.
In practice, we model not the density but the volumetric
absorption cross-section 
(r,z). We will assume
that the same functional form can be used, however, and
complete our description of (r,z) with a reference
value 0 =(R0 =1 AU,z=0).
The complete description of the volumetric absorption cross-section is then
(r,z) = 0(R0/r)
×
exp[- (|z|/r)]
cm-1 (1)0, , , and are free parameters,
R0 = 1 AU, and (r,z) are cylindrical coordinates.
G.3.b Temperature
Gray particles (with diameters >> wavelength and constant albedo with heliocentric distance) when heated by the Sun will give rise to an equilibrium temperature that varies as R-0.5. However, variation of properties with distance or wavelength will disturb this ideal case. Consequently, in this study we allow the temperature to vary as R-
where is a free
parameter. The temperature at 1 AU (T0) is also free. It is
assumed that a constant with heliocentric distance is
sufficient to deal with local dust properties.
The complete description of the temperature is
K (2) are free parameters (and R is
the radial distance from the Sun).
G.3.c Emissivity
The emission behavior of solid particles in the infrared is complex and the breadth of the IRAS band passes precludes making any definitive statements about composition. However, it became clear from the fitting that a long wavelength emissivity drop-off was necessary to attenuate the 60 and 100 µm model predictions (a flat emissivity produced too much flux in these bands). Models of dust grain properties (Roser and Staude 1978) indicate that typical materials are reasonably constant in the 10 to 25 µm region but fall off as
-
(where = 1-3) for longer
wavelengths. Consequently, this study has used an emissivity
that is constant out to some cutoff (0) and then drops
as -. In practice, even this is a level of
complication unwarranted by the data and the two parameters,
0 and , cannot be fit simultaneously (they are too
strongly correlated). We therefore arbitrarily chose to let
= 1 (Mie theory for spherical particles). This
approximation will be shown to have no effect on any of the
parameters other than 0.
The complete description of our model for the emissivity is
= 0
<= 0=
0(/0)-1 > 0 (3)0 is a parameter.
In practice, 0 is an unknown and will be
subsumed by n0, the volumetric absorption cross-section.
G.3.d Cloud Orientation
The zodiacal dust cloud is assumed to be azimuthally symmetric but is allowed to have an inclination relative to the ecliptic. This introduces two more free parameters: the inclination angle i and the line of ascending nodes
. The assumption of azimuthal symmetry
will be in error if the cloud is warped and thus
has different inclinations/lines of nodes in different parts
of the solar system (Misconi 1980). We should,
however, be able to detect the presence of such discrepancies
in the residuals to the fit as a function of solar elongation.
G.3.e Constant Background
It became apparent during the fitting that the shape of the zodiacal emission could only be fit if a baseline offset were introduced in each band. The origin of this extra flux is unclear; it could be a calibration offset, or it might represent an isotropic background component on the sky. A detailed comparison with the ZIP (Murdock and Price 1985) or COBE data may resolve this uncertainty.G.3.f Model Parameters
There are thus a total of fourteen free parameters in our model (four for the density, two each for the temperature, the emissivity, and the cloud orientation, and four for the background). However, as mentioned previously, it is impossible to derive values for both of the emissivity parameters simultaneously and, therefore, the total number of parameters is reduced to 13. Although this number of parameters may seem excessive, the number of degrees of freedom is large [~200 (scans)× 360 (samples)× 4 (bands)]. It will be shown that these parameters are sufficiently uncorrelated to make a unique solution possible.G.4 Fitting Procedure
It is relatively simple to generate a model that is capable of fitting one wavelength of one scan. Such a fit gives a moderately good estimate of the parameters defining the z-dependence of the density but does not do well on the radial dependence of density or temperature and is insensitive to the cloud inclination and line of nodes.To determine the cloud orientation parameters requires several scans spread out over the full time range of the mission (equivalently, the range of Earth orbital longitudes). In addition, to determine accurately the radial dependence of density and temperature requires the use of the full range of solar elongation angles. Finally, to constrain fully the temperature and to estimate the emissivity properties we must fit all four bands at once. Preliminary fitting with a subset of our model and of the data (Good, Hauser and Gautier 1986) gave credible values for those parameters fit but with much higher uncertainties than the present effort and with a poorer fit (further emphasizing the need for the full parameter set).
In addition to its inability to constrain all the model parameters, a single scan is contaminated by some unknown amount of Galactic light. It is impossible to separate out a smooth Galactic component in one scan, but if two scans covering the same position on the celestial sphere are observed at different times (i.e., through different amounts of the zodiacal dust cloud), fitting to both scans simultaneously will implicitly be sensitive to time variability, which can only be due to the cloud.
We are therefore forced to the conclusion that an accurate
derivation of the cloud parameters requires
simultaneous fitting to the full subset of scans described
above. The procedure used in the fitting is a) to
generate model estimates of all 200 scans using a given set
of model parameters, and b) to adjust the parameters
using the method of least squares
until the best fit is achieved.
The flux integral along any line-of-sight is given by
Fo (,
,t) =
minmax
Ro()
0linfinity
(rc,zc)B(T(R))
dl d (4)
where and are the elongation and inclination
of the observation, (r,z) and T(R) are as described
above [with (rc, zc in cloud coordinates, not ecliptic)].
B(T) is the Planck function, Ro()
is the spectral response of the detector/filter combination
with nominal wavelengths 0= (12, 25, 60 or 100 µm) and
l is the unit vector in the direction (, ) at time t.
Positions in (rc, zc)-space are calculated from (l, ,
) taking into account the orbital position of the Earth at
time t (including eccentricity of the Earth's orbit) and the
orientation of the dust cloud.
To generate the model scans, the flux from the model cloud was integrated along several lines of sight and over the bandpass. Thirteen reference points were used for each scan, spread out between inclination angles -90° and +90° but concentrated toward the ecliptic plane where the variation was most extreme. The resultant flux for the reference points was interpolated, using a cubic spline under tension, to give model fluxes for each of the real data points. The difference between this interpolated function and a full flux integration is typically less than 0.05%.
Each parameter in the model (the thirteen described above) was then perturbed slightly. The variations of the model with respect to these perturbations and the differences between the nominal model and the real data were then combined to generate updates to the estimated model parameters. This procedure was iterated until the parameters converged.
As mentioned previously, the fluctuations above the zodiacal background are not noise but Galactic structure. Consequently, those points that are strong positive excursions from the model (when the model has become reasonably accurate) should be given a very low weight to exclude the galaxy and the zodiacal dust bands. Such a weighting can be incorporated into the least-squares process since an uncertainty for each point is part of the scheme. Without this "lower envelope" approach the fit would be biased, especially at the longer wavelengths, by the Galactic emission.
G.4.a Model Results
The results of fitting our model to the 200 scans are shown in Table G.1 and the coefficients of correlation between the parameters are shown in Table G.2. Representative scans (for several elongations and times) are shown in Figures G.4, G.5 and G.6. Considering the number of parameters, even the highest of the correlations (0.91, between the power law exponents on and T)
is quite small. We therefore conclude that the
inclusion of all the free parameters in our model is justified
and, moreover, that they are all required to fit the data properly.
| Class of Parameter | Values of Parameters | Units |
|---|---|---|
| Density | 0=1.439±0.004 × 10-20 =1.803±0.014 =4.973±0.024 =1.265±0.003 |
cm-1 unitless unitless unitless | Temperature | T0 = 266.20± 0.18 =0.359 ±0.004 |
Kelvin unitless |
| Emissivity | 0=37.75± 0.09=1 |
µm (fixed) |
| Orientation | O=68.61 ±0.03 i=1.73±0.01 |
degrees degrees |
| Offsets | 12 µm=35.53 ±0.15× 10-8 25 µm=49.97± 0.14× 10-8 60 µm=2.19 ± 0.03× 10-8 100 µm=5.24± 0.07× 10-8 |
Wm-2sr-1 Wm-2sr-1 Wm-2sr-1 Wm-2sr-1 |
|
|
|
Figure G.4 A typical IRAS pole-to-pole scan
with the zodiacal dust cloud model fit (solid line).
This scan was at a solar elongation of 90°. The
zodiacal dust bands are visible as bumps at the ecliptic plane
(inclination 180°) and at ± ~ 10°. The
remaining structure is Galactic emission. larger largest |
|
|
|
Figure G.5 Data and zodiacal dust cloud
model prediction for a scan
at solar elongation of 112°.
The profiles are broader and less intense than those in Figure
G.4 since this scan is looking through material farther from the Sun,
which is both cooler and has a larger z scale height. larger largest |
|
|
|
Figure G.6 Data and zodiacal dust cloud model
prediction for a scan
at solar elongation of 67°.
The same discrepancy noted in Figure G.5 exists for these data.
These profiles are narrower and more intense since this scan is
observing material closer to the Sun. larger largest |
| Parameters | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Offsets (µm) | 0 |
|
|
|
T0 | |
0 |
|
i | |||
| 25 | 60 | 100 | ||||||||||
| -.11 | 0.00 | 0.00 | 0.30 | 0.24 | 0.24 | 0.18 | -0.44 | -0.26 | 0.00 | -0.05 | -0.01 | 12µm |
| 0.06 | 0.01 | -0.52 | -0.28 | 0.27 | 0.19 | 0.56 | 0.32 | 0.34 | -0.11 | 0.04 | 25µm | |
| 0.03 | -0.06 | -0.08 | 0.04 | 0.03 | 0.08 | 0.09 | -0.31 | -0.04 | -0.01 | 60µm | ||
| -0.02 | -0.02 | 0.01 | 0.01 | 0.02 | 0.02 | -0.05 | -0.01 | 0.00 | 100µm | |||
| 0.73 | 0.25 | 0.0 | -0.86 | -0.55 | -0.17 | 0.14 | -0.19 | 0 | ||||
| 0.31 | 0.20 | -0.77 | -0.91 | 0.12 | 0.06 | -0.16 | | |||||
| 0.89 | -0.08 | -0.08 | 0.1 | -0.47 | -0.19 | | ||||||
| -0.06 | -0.11 | 0.12 | -0.56 | -0.10 | | |||||||
| 0.78 | 0.18 | -0.09 | 0.11 | T0 | ||||||||
| -0.09 | -0.05 | -0.09 | | |||||||||
| -0.0 | -0.05 | 0 | ||||||||||
| -0.09 | | |||||||||||
The complete volumetric emissivity distribution description is given by
= 1.43 × 10-20 (R0/r)1.80exp[-4.97z/r1.26]
cm-1 (5)
The emissivity properties of the dust material are extremely
uncertain, although their overall emissivity
is probably quite high. Models of
the absorption/emission behavior for various
materials (Roser and Staude 1978) show that several likely
candidates for the dust (eg., olivine, obsidian)
have fairly flat (though very uneven) emission properties between
about 10 and 30 µm but then drop
off as -n (n=1-3) out to beyond 100 µm.
Our approximation is very crude, but the results of our fit
require a decreasing emissivity at long wavelength and
relatively flat emissivity between 10 and 30 µm.
The large width of the IRAS filters precludes finer analysis
of the composition of the dust.
References
Briggs, R.E. 1962, Astron. J., 67, 710.
DIRBE Explanatory Supplement 19 July 1993, distributed by National
Space Science Data Center (NSSDC).
[Present version 2.3]
Leinert, C., M. Hanner, and E. Pitz 1978a, Astron. Astrophys., 63, 183.
Leinert, C., M. Hanner, H. Link and E. Pitz 1978b, Astron. Astrophys., 64, 119.
Leinert, C., M. Hanner, I. Richter, and E. Pitz 1980, Astron. Astrophys., 82, 328.
Leinert, C., I. Richter, E. Pitz, and B. Planck 1981, Astron. Astrophys., 103, 177.
Misconi, N.Y. 1980, "The Symmetry Plane of the Zodiacal Cloud Near 1 AU", in Solid Particles in the Solar System, eds. I. Halliday and B.A. Mclntosh, (Reidel:Dordrecht), 49.
Mukai, T., and R.H. Giese 1984, Astron. Astrophys., 131, 355.
Murdock, T.L. and S.D. Price 1985, Astron. J., 90, 375.
Roser, S., and H.J. Staude 1978, Astron. Astrophys., 87, 381.
Trulsen, J., and A. Wikan 1980, Astron. Astrophys., 91, 155.