IRAS Explanatory Supplement
VIII. Sky Coverage, Confusion, Completeness and Reliability
C. Point Source Confusion
Chapter Contents | Authors | References
Table of Contents | Index | Previous Section | Next Section
Suppose that the mean density N(fv) of sources on the sky with flux density greater than fv obeys a power law:
(VIII.C.1) where a (<0) is a constant. In a small interval in flux density
(fv,
fv +
dfv) and within a beam of solid
angle
(VIII.C.2)
Equation (VIII.C.2) can be used to estimate the
effect of confusion on the IRAS survey in two ways. first, the confusion
noise can be calculated directly from the equation using the observed density
and distribution of sources. Differential sources counts,
dN/d(log fv),
are given in Fig. VIII.C.1a-d for sources in all
wavelength bands with |b| > 50°. The plots demonstrate that at
high
Galactic latitudes, objects detected at 12 and 25 µm follow
a power law distribution (Eq. (VIII.C.1)) with an index
a equal to -1.0 and that sources brightest at 60 µm, mostly
external galaxies, have a equal to -1.5. Sources brightest at 100 µm
do not follow a simple power law due to the effects of cirrus and will
be discussed separately in Section VIII.D.5. The
typical source density for sources at 12, 25 and 60 µm with
flux densities brighter than 0.5 Jy is 0.6 source per sq. deg at high Galactic
latitudes. for typical detector areas the noise level due to confusion
as calculated using Eq. (VIII.C.2) is -15 mJy, far
below the instrumental detection limits.
one expects on average
a
N(fv)
fv-1
dfv sources. The actual number will
be a stochastic variable with a mean-squared deviation equal to the average
value. The mean-squared deviation in the flux will be
fv2 × the deviation in the
number. Thus the mean-squared flux deviation,
(
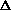fv)2,
from all sources below some threshold fv0
is given by
 |
|
Figure VIII.C.1 Differential source counts as a function of flux density
for the four wavelengths sources with Galactic latitudes |b| . 50°. larger largest |
The second way to interpret Eq. (VIII.C.2) is to
note that the critical term in determining the importance of confusion
is the product
N
which is the total number of sources per beam area. At high Galactic latitudes,
the observed value of N
is less than 0.001 sources per beam for sources above the threshold of
0.5 Jy. The source densities over the whole sky for the four wavelength
bands are shown in Figs. V.H.1.1-1.4. At
the transition between the white and grey areas of these figures, the source
density is less than 1 per 50 beams; this means that the confusion noise
at the transition is less than 0.2 of the completeness limit at all wavelengths.
Confusion noise can therefore be ignored in the white areas of
Fig. V.H.1.1-.1.4.
At 100 µm the shape of the unconfused regions is irregular and
artificial due to the presence of infrared cirrus; the entire sky except
at the highest Galactic latitudes can be confusion limited due to local
infrared cirrus. In the darker areas of these figures confusion noise
dominated
the source recognition process, as will be discussed in
Section
VIII.D.5.
A signal-to-noise ratio of five which corresponds to the IRAS completeness
limits at 12, 25 and 60 µm would, according to Eq.
(VIII.C.2), be achieved at 75 beams per source for a = -1.5 and
at 25 beams per source for a = -1.0. This latter value was used as
the confusion limit for the high source density processor.
Chapter Contents | Authors | References
Table of Contents | Index | Previous Section | Next Section