IV. 2MASS Data Processing
5. Extended Source Identification and Photometry
a. Introduction
The extended source sensitivity (10 ) is
~1 mag brighter than the point source limits, or
14.7 (2.1 mJy), 13.9 (3.0 mJy), and 13.1 (4.1 mJy) mag at J, H, Ks,
respectively, with the precise threshold depending on the brightness profile
of the extended source. Given the ~2´´ angular
resolution of the image data and the detector sensitivity, 2MASS is well
suited for detecting most types of galaxies to cz < 10,000 km/s and high
luminosity giant galaxies beyond 30,000 km/s. In addition to galaxies, 2MASS
will also identify compact and diffuse Galactic objects. The 2MASS catalogs
are expected to detect over 100 million stars and greater than 1 million
galaxies.
) is
~1 mag brighter than the point source limits, or
14.7 (2.1 mJy), 13.9 (3.0 mJy), and 13.1 (4.1 mJy) mag at J, H, Ks,
respectively, with the precise threshold depending on the brightness profile
of the extended source. Given the ~2´´ angular
resolution of the image data and the detector sensitivity, 2MASS is well
suited for detecting most types of galaxies to cz < 10,000 km/s and high
luminosity giant galaxies beyond 30,000 km/s. In addition to galaxies, 2MASS
will also identify compact and diffuse Galactic objects. The 2MASS catalogs
are expected to detect over 100 million stars and greater than 1 million
galaxies.
The scientific objectives of the extended-source portion of 2MASS include studies of large scale structure, utilization of the infrared Tully-Fisher relation, a complete survey of the local group of galaxies, and an unprecedented census of galaxies located behind the plane of the Milky Way, often referred to as the "Zone of Avoidance." As such, survey requirements were established in order to satisfactorily achieve these science goals. In addition to the sensitivity limits given above, the extended source Level 1 Specifications include >90% completeness and >98% reliability for most of the sky (free of stellar confusion). There are no set requirements for observations deep in the Galactic plane, but the survey maintains a high level of utility all the way down to |b| ~ 0° (Jarrett et al. 2000a, AJ, submitted). The Level 1 science requirements apply to the galaxy catalog derived from the 2MASS database.
The basic 2MASS data and pipeline reduction overview, including discussion of the point spread function - a basic component of star-galaxy separation - is given here. We also describe the key parametric measurements made on extended sources and the crucial operational step of background removal. In addition, we describe the algorithms developed to cleanly discriminate between point sources and extended sources. The catalog reliability criterion is, in particular, a difficult goal to achieve, necessitating implementation of algorithms specifically designed to perform star-galaxy separation with 2MASS imaging data. Finally, we give some examples of the wide array of extended sources that 2MASS detects. We will present more detailed scientific results from the 2MASS catalog, including galaxy colors, source counts, completeness and reliability, and clustering in a future paper, Jarrett et al. (2000b, in preparation).
b. Data and Basic Reductions
i. Image Data
The 2MASS survey strategy is to map the sky with overlapping strips, or tiles, each of approximately 6° in length and 8.5´ in width, using three (one for each band) 256 × 256 NICMOS (HgCdTe) arrays (2´´ pixels). The data are efficiently acquired with a freeze-frame scanning technique (detailed in Beichman et al. 1998, PASP, 110, 480), such that every piece of sky is observed a total of six times at 1.3 s of integration per sample. With careful sub-pixel dithering between samples, the deleterious effects of under-sampling are minimized. Frames are optimally combined to form "Atlas" images of size 512 × 1024 pixels with resampled 1´´ pixels; hence, 8.5´ × 17´ images. Each 6° scan is comprised of ~23 Atlas images. Atlas images have ~10% overlap, ~51´´, along the in-scan (declination) axis to minimize incompleteness of large galaxies. The Atlas image is the basic data product from which galaxies and extended sources are detected, characterized and extracted into the 2MASS database. In addition to the full Atlas images, small subsections of the Atlas images (referred to as "postage stamp" images) are extracted for each extended source (see below).
ii. Pipeline Reductions Overview
High level data reductions include linearity, dark frame subtraction and pixel-to-pixel gain correction (i.e., flat-field correction), which are formed in a non-standard fashion to accommodate the data set unique to the 2MASS survey (see the 2MAPPS Functional Design Document 1996; Beichman et al. 1998, PASP, 110, 480; Cutri 1997, in "The Impact of Large Scale Near-IR Sky Surveys"). Further pipeline reductions include frame-to-frame offset determinations, simple background subtraction, source detection, atmospheric "seeing" and point spread function (PSF) characterization, stellar photometry, band merging, artifact removal, accurate position reconstruction, and photometric calibration. The source detection step described below is vital to both point source processing and extended source processing. The extended source processing occurs at the end of the 2MASS data reduction pipeline. The main objective of the 2MASS extended source processor, referred to as GALWORKS, is to parameterize source detections and determine which sources are "extended" or resolved with respect to the PSF. Consequently, one of the many vital operations for successful star-galaxy discrimination is the accurate measurement of the PSF.
iii. Source Detection
The primary 2MASS source detection procedure is designed to locate both point
sources (primarily stars) and extended sources (primarily galaxies).
The detection thresholds are chosen to assure complete detection of galaxies
brighter than the Level 1 specification, Ks ~ 13.5 and J ~ 15 mag,
over a wide range in surface brightness. For fainter low surface brightness
galaxies the completeness will steadily fall off with flux, hence a separate
detection step is carried out to find these objects (see
below).
The detection algorithm is closely modeled after the DAOPHOT FIND algorithm
(Stetson 1990, PASP, 102, 932) which was devised to find stars over a wide
range of stellar
number density. Each Atlas image is convolved with a 4´´ FWHM
Gaussian over a 13 pixel sub-array averaged to zero. The
resulting zero-sum filtered image is set at a threshold of ~3 times the
estimated noise level for the Atlas image, with detections corresponding to
each central maximum within a threshold region. A rough position and flux is
estimated from the corrected (convolved image) centroid. The detection list is
then fed to a PSF characterization task (see below)
and finally to a PSF
profile-fitting photometry processor, where positions and integrated fluxes
are refined. The detection thresholds (3
iv. Data Anomalies and Artifacts
Data anomalies and image artifacts come in a variety of flavors, including
those from the local environment (Observatory and atmosphere), space (meteor
streaks, bright stars), from the equipment (array detectors and electronics,
telescope tracking and focus), and from the software (algorithm and pipeline
defects). Extended sources are vulnerable to most of these problems, but in
particular those in which the image backgrounds are corrupted. For example,
bright stars (Ks < 7 mag) induce several different
image artifacts, including confusion halos, large-angular extent diffraction
spikes, horizontal striping, persistence ghosting, reflection glinting, and
large-scale background corruption for the brightest stars (K <
3 mag). Detection and removal of artifacts is a high priority in
the reduction pipeline software and post-processing catalog generation. Still,
it is not possible to eliminate all artifacts from the image and source
products. Further discussion of data anomalies and artifacts is given
below.
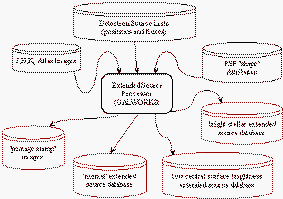
The last major subsystem to run in the 2MASS quasi-linear data reduction
pipeline is the extended source processor,
GALWORKS. The primary role of the processor is to
characterize each detected source and decide which sources are "extended" or
resolved with respect to the point spread function (PSF). Sources that are
deemed "extended" are measured further and the information is output to a
separate table. In addition to tabulated source information, a small "postage
stamp" image is extracted for each extended source from the corresponding J, H
and Ks Atlas images. The source lists and image data are stored in
the 2MASS extended source database. The basic input/output flow is
shown in Figure 1.
By the time GALWORKS is run in the 2MASS
pipeline, point sources have been fully measured with refined positions and
photometry, band-merged, coordinate positions calibrated, Atlas images
constructed, and the time-dependent PSF characterized for every Atlas image.
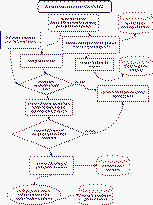
The high-level steps that encompass GALWORKS
include: (1) bright star (and their associated features) removal, (2) large
(>4´) cataloged-galaxy extraction and removal,
(3) Atlas image background subtraction, (4) measurement of the stellar number
density and confusion noise, (5) source parameterization and attribute
measurements, including generation of PSF-tracking ridgelines, (6) star-galaxy
discrimination, (7) refined photometric measurements, and finally (8) source
and image extraction; see flow schematic in
Figure 2. Additional post-pipeline
processing are carried out to produce complete and reliable catalogs,
which are released to the public.
 )
correspond to J~16 mag for point sources. For such faint sources,
the implied extended source threshold is only ~0.5 mag brighter, producing a
list of sources much fainter than the extended source requirements. Extended
sources are ultimately identified from this inclusive detection source list.
)
correspond to J~16 mag for point sources. For such faint sources,
the implied extended source threshold is only ~0.5 mag brighter, producing a
list of sources much fainter than the extended source requirements. Extended
sources are ultimately identified from this inclusive detection source list.
c. The Extended Source Processor
|
 |
| Figure 1 | Figure 2 |
2MASS is an all-sky project that will acquire something like ~40 Tb of data over the lifetime of the project. This places severe runtime restrictions on the pipeline reduction software; consequently, one important caveat is that most of the GALWORKS algorithms and flow structures were designed specifically to run and operate as fast and as efficient as possible, with some functionality omitted toward this end (e.g., orientation modeling). The background subtraction operation is a particularly crucial step since both star-galaxy discrimination and photometry rely upon accurate zeroing, smoothing and flattening of the image background. This operation is described in detail below. Steps 4-6 are designed to isolate "normal" galaxies and other relatively high central surface brightness extended sources.
The 2MASS extended source database contains several classes of "extended objects," including real galaxies, Galactic nebulae and pieces of large angular-size sources, Galactic H II regions, multiple stars (mostly double stars), artifacts (pieces of bright stars, meteor streaks, etc.) and faint (mostly point-like) sources with uncertain classifications. For extended sources, the ultimate goal of the 2MASS project is to produce a reliable catalog of real extended sources, predominantly galaxies. It is therefore necessary for additional "post-processing" steps to eliminate artifacts and confusing objects like double stars. We discuss here and here in detail how the star-galaxy separation process is performed. For the GALWORKS processor, the emphasis is placed primarily on completeness; that is, we want to comprehensively detect and identify extended sources (especially galaxies) brighter than the Level 1 specifications limits of Ks ~ 13.5, H ~14.3 and J ~15.0 mag. Later in the (non-GALWORKS) post-processing operations phase the galaxy completeness is relaxed (but still within the Level 1 requirements) in order to achieve the desired reliability in the galaxy catalog.
There are other kinds of extended sources that 2MASS is capable of detecting, including bright Galactic young stellar objects (H II regions, T-Tauri stars, etc.), faint nebulae and low surface-brightness (LSB) galaxies. These objects tend to be relatively rare and/or constrained to relatively small angular-sized fields toward the Galactic plane (e.g., molecular clouds) and as such there are no set requirements for their detection completeness or reliability. A separate catalog of bright extended stars and faint LSB galaxies will be released at a later date. A description of the algorithm to detect stars with associated extended emission and the algorithm to detect low central surface brightness galaxies are described below.
i. Atlas Image Background Removal
In the near-infrared, the background "sky" emission has structure at all size
scales, primarily due to upper atmospheric aerosol and hydroxyl emission (the
so-called "airglow" emission; see Ramsey et al 1992). The OH emission is the
dominant component to the J (1.3 µm) and H-band (1.7 µm)
backgrounds, while thermal continuum emission comprises the bulk of the
Ks (2.2 µm) background. The J and H images tend to
have more background "structure," and at times of severe airglow, the
background can have high frequency features on scales of tens of arcseconds
that can trigger false extended source detections. For extended sources, the
primary objective of the 2MASS project is to find and characterize galaxies
(and other extended objects) smaller than ~3´ in diameter. We
therefore attempt to remove airglow features slightly larger than this limiting
size scale to minimize random and systematic photometric error from non-zero
background structure. This demands a more sophisticated fitting scheme then
median filter or grid techniques allow (used, for example, in SExtractor, from
Bertin & Arnouts 1996, A&AS, 117, 393). For the most part, the
background variation in a
given image (8.5´ × 17´) is smooth enough that it can be
modeled with a polynomial. A third order polynomial turns out to be a good
compromise between a simple planar fit and a series of spline waves. The
fitting procedure is first preceded by an image "clean" operation. Stars and
catalogued galaxies are masked from the image. Very bright stars
(K < 6 mag) require more complicated masking, including removal of their
bright internal reflection halo, diffraction spikes, horizontal streaks,
filter glints and persistence ghosts.
The background removal process is applied separately to each J, H,
and Ks Atlas image. Given the 2:1 image aspect ratio, the
"cross-scan" (E-W) length, ~8.5´, represents the
maximum area that can be modeled. Accordingly, a cubic polynomial,
ax3 + bx2 +cx + d, provides an effective model
for smooth background variations larger than ~2´ to 3´.
Along the 17´ "inscan" (N-S) direction we subdivide
the array into three sections, consisting of lower and upper 512´´
blocks, and a central 512´´ block. The central block acts as the
"glue" that smoothly joins the boundaries of the two lower/upper background
solution sections. The final 512 × 1024 pixel composite
solution is generated from a weighted average of each 512 × 512-block
solution. The median value of the composite background solution for each band
is extracted and tabulated in the 2MASS database (and catalog), identified as
"<band>_sky", where <band> refers to
either the J, H or Ks Atlas image. The median value of the
background solution local to a particular extended source is called
"<band>_back" in the database. The average
"noise" in the background-subtracted (and star masked) Atlas image is derived
from the average of the 16% and 84% histogram quartile values in the pixel
value distribution. In this way the derived "noise" is analogous to a
1-
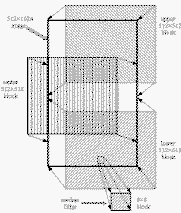
The decomposition schematic for background fitting procedure is illustrated in
Figure 3.
The 512 × 1024 Atlas image is represented by a thick-lined
rectangle. The image is separated into three 512 × 512 pixel sections.
The image sections are then smoothed with an 8 × 8 pixel median filter,
to minimize contamination from faint stars and point-like objects that escaped
the masking "clean" procedure (see above). Using a least-squares technique, a
cubic polynomial is iteratively fit with 3
Representative performance of the background removal operation is shown in
Figure 4. The image data comes from a
not-atypical "photometric" northern hemisphere night. Note the significant
"airglow" emission during the period that this data was acquired (see H-band,
middle panels). The figures show the "raw" Atlas Image, resultant background
solution and residual (background subtracted) image. The gray-scale stretch
ranges from -2
For the case in which the airglow frequency of variation is higher than can
be adequately removed, the resultant photometry (particularly at H band) is
severely compromised. These data are given a lower quality score and are
scheduled for re-observation if time permits. Inevitably, there will remain
cases in which residual airglow in the background-removed images significantly
distorts the H-band photometry (and possibly at J-band as well) but otherwise
goes unrecognized in the quality review process.
 RMS measurement. The pipeline extracted
parameter identification is "<band>_bkgnd_sig_his", representing
the "noise" of the background-removed Atlas image.
RMS measurement. The pipeline extracted
parameter identification is "<band>_bkgnd_sig_his", representing
the "noise" of the background-removed Atlas image.
 rejection to each smoothed line within a section. The line solutions are used
as input to the next step, where we fit a cubic polynomial to each column in a
section, thereby coupling the line and column background solutions. The three
section solutions are then joined with a
(1/
rejection to each smoothed line within a section. The line solutions are used
as input to the next step, where we fit a cubic polynomial to each column in a
section, thereby coupling the line and column background solutions. The three
section solutions are then joined with a
(1/ r) taper. Here
r) taper. Here
 r refers to the relative radial
("in-scan") difference between
any two given section solutions. So for example, combining the lower and
central sections at some point, Y' (which ranges
from 256 to 512 corresponding to the overlap region) gives the respective
weights [1 / | 256-Y' |] and
[1 / | 512 - Y' |], and for the central and upper sections
the respective joining weights are [1 / | 512-Y' |] and
[1 / | 768 - Y' |], where
Y' ranges from 512 to 768. With this technique we are able to smoothly
combine the three independent solutions per Atlas image. Note
however, the boundary solutions for the upper and lower blocks are better
constrained near the center of the image due to the weighted addition of the
central block solution image. Conversely, the background solutions are not as
well determined at the upper, >896 pixel row, and lower, <128 pixel row,
"in-scan" image extremes.
r refers to the relative radial
("in-scan") difference between
any two given section solutions. So for example, combining the lower and
central sections at some point, Y' (which ranges
from 256 to 512 corresponding to the overlap region) gives the respective
weights [1 / | 256-Y' |] and
[1 / | 512 - Y' |], and for the central and upper sections
the respective joining weights are [1 / | 512-Y' |] and
[1 / | 768 - Y' |], where
Y' ranges from 512 to 768. With this technique we are able to smoothly
combine the three independent solutions per Atlas image. Note
however, the boundary solutions for the upper and lower blocks are better
constrained near the center of the image due to the weighted addition of the
central block solution image. Conversely, the background solutions are not as
well determined at the upper, >896 pixel row, and lower, <128 pixel row,
"in-scan" image extremes.
 to
5
to
5 of the mean background
level (where
of the mean background
level (where  is the background "noise"
derived from the background-removed Atlas image pixel histogram; see above).
The J, H, and Ks raw images reveal fairly low level (smooth, but
non-linear) background variations, while the corresponding residual images
show very little (if any) background structure. However, airglow emission is
much more prevalent in the H-band, with size scales smaller than
~1´-2´, as evident in the residual image. It is this
residual structure in the background (with amplitude >10% of the mean
background noise) that can induce systematics in the photometry,
parameterization (e.g., azimuthal ellipse fitting), and reliability.
is the background "noise"
derived from the background-removed Atlas image pixel histogram; see above).
The J, H, and Ks raw images reveal fairly low level (smooth, but
non-linear) background variations, while the corresponding residual images
show very little (if any) background structure. However, airglow emission is
much more prevalent in the H-band, with size scales smaller than
~1´-2´, as evident in the residual image. It is this
residual structure in the background (with amplitude >10% of the mean
background noise) that can induce systematics in the photometry,
parameterization (e.g., azimuthal ellipse fitting), and reliability.
|
 |
| Figure 3 | Figure 4 |
ii. Source Positions
In addition to the coordinate position based on the PSF-fit operation, two additional "extended source" positions are computed. The first is based upon the peak pixel from the J-band image, where 2MASS is most sensitive (except when dust extinction is appreciable). The precision of the peak-pixel coordinate is limited by the 2´´ resolution and convolution method used to construct/resample Atlas images from raw frames. Based on internal repeatability tests and external comparisons with astrometrically accurate galaxy catalogs (see Jarrett et al 2000b, in preparation), these coordinate positions possess a RMS uncertainty of ~0.5´´. They are identified in the 2MASS database as "ra" and "dec". The second is based upon the intensity-weighted centroid of the J+H+Ks "super" Atlas image. The "super" centroid coordinate position is usually more precise since it applies a 2-D centroid to higher SNR data, but it can be more influenced by unusual morphologies and extinction. Based on repeatability tests, the estimated uncertainty of the "super" centroid position is ~0.3´´ for normal surface brightness galaxies. The database names are "sup_ra" and "sup_dec".
iii. Ellipse Fitting and Object Orientation
The 2MASS undersampling and runtime constraints limit fitting an ellipse to
a single surface brightness isophote in each band. To minimize the effect of
PSF elongation and to best approximate the mean orientation of the
galaxy being measured, the isophote to be fit corresponds to a surface
brightness ~three times the background noise (3
Using only one isophote to represent the shape of a galaxy is clearly an
approximation since galaxies can change orientation with radius. But, in the
near-infrared most galaxies appear to have somewhat more consistent
orientations and axis ratios at different radii owing to the relatively smooth
distribution of stars that dominate the 2µm light
and the decreasing importance of extinction at these wavelengths. Moreover,
most 2MASS galaxies are small in size (~15´´ in diameter), so for
our ~2´´ angular resolution, multiple fits are not especially useful.
In addition to requiring that the ellipse-fitting method run fast, it also
must be robust in the presence of confusion from nearby sources (i.e., stars)
and correlated noise features that form "extended" limbs and other disconnected
extended features. We do this by carefully masking neighboring sources when
the stellar source density is high (see below), and removing linear 1-pixel
wide "limbs" that extend outward from the primary
3
Once we have isolated the 3
An additional fit is performed on the combined (J+H+Ks) "super"
Atlas image. In general, the "super" Atlas image has a higher signal-to-noise
ratio than the individual fits. Accordingly, the derived "super" Atlas image
orientation serves as the "default" shape for cases in which the individual
band flux is fainter than: ~14.4 mag at J, ~13.9 mag at H and ~13.5 mag at
Ks, or when the S/N ratio of the galaxy is less than
5.0, based on the R=10´´ fixed circular aperture
photometry. For the case in which the derived semi-major radius is less than
5´´ or greater than 70´´, the source is assumed to be
round and the axis ratio parameter is set to unity. For the case in which the
derived axial ratio is less than 0.10, the ellipse fit parameters are set to
the corresponding fit from the "super" Atlas image. Finally, the "super" Atlas
image values are also used when the individual band fit for one reason or
another is not possible (e.g., when masked pixels are present within
1´´ of the peak pixel). The database names are "sup_ba",
"sup_phi", "sup_r_3sig", and "sup_chi_ellf".
A final note regarding the ellipse fitting operation relates to
nearby-neighbor masking. Bright disk galaxies (Ks < 12.5 mag) in
which the inclination is large (>40°), are apt to be "split" into
multiple point sources by the initial source detector (discussed
above).
Consequently, we do not perform any stellar masking or subtraction specific to
the ellipse fitting step, except when the stellar number density is
high, >2000 stars deg-2 for Ks < 14 mag, in which
case it is more favorable to mask out nearby stars
given the high probability of contamination. This ellipse-fitting detail
should not be confused with the general GALWORKS
procedure of near-neighbor masking prior to photometry or radial-symmetry
measurements.
iv. Photometry
Given the assorted shape, size and surface brightness that galaxies exhibit
in the near-infrared, a corresponding diverse array of apertures is used to
compute the integrated fluxes. Contamination from stars within or near the
aperture boundary is minimized with pixel masking-but still remains
significant when the confusion noise is high. Flux from masked pixels is
"recovered" with isophotal substitution, where the mean value of the elliptical
isophote (based on the elliptical shape parameters, b/a and
The simplest measures come from fixed circular apertures. Fluxes are
reported for a set of fixed circular apertures at the following radii: 5, 7,
10, 15, 20, 25, 30, 40, 50, 60, and 70´´,
centered on the J-band peak pixel. (Note: the large set of apertures was
chosen so that the user could generate a curve of growth to estimate the total
flux). We report both the integrated flux within the aperture (with fractional
pixel boundaries) and the estimated uncertainty in the integrated flux. The
magnitude uncertainty is based solely on the aperture size and the measured
noise in the Atlas image, which includes both the read-noise component and
background Poisson component, as well as the confusion noise component, which
becomes significant when the stellar source density is high (see
Appendix B).
The uncertainty does not incorporate other errors due to source
contamination, background gradients (e.g., airglow ridges with a higher spatial
frequency than the background removal process can handle; see
above),
zero-point calibration error, and uncertainties in the adaptive apertures
(e.g., isophotal photometry, see below). A more detailed discussion of the
2MASS galaxy photometry error tree can be found in Appendix A. Contamination,
confusion and masking flags are also attached to each flux. In the 2MASS
database the photometry names are, for example, "<band>_m_10",
"<band>_msig_10", and "<band>_flg_10", for the
10´´ radius aperture photometry, uncertainty and
confusion flag names, respectively.
For the great majority of faint galaxies in the 2MASS catalog, small fixed
circular apertures give the best compromise between increasing noise, due to
confusion and missing flux in the faint outer parts of galaxies. In particular,
the circular 7´´ radius aperture appears to have
the optimum match with the coupling between the 2MASS undersampling and PSF
elongation, with the H and Ks background noise, and with the size
of galaxies fainter than Ks~13 mag.
Adaptive aperture photometry includes isophotal and Kron metrics. The
isophotal measurements are set at the 20 mag per arcsec2 surface
brightness isophote at Ks and the 21 mag per arcsec2 at
J, using both circular and elliptically shape-fit apertures (see previous subsection). Kron aperture photometry (Kron 1980,
ApJS, 43, 305) employs a method in which the
aperture is controlled/adapted to the first image moment radius. The Kron
radius, which is frequently used in galaxy photometry as a "total" measure of
the integrated flux (Koo 1986, ApJ, 311, 651; Bertin & Arnouts 1996,
A&AS, 117, 393), turns out to
roughly correspond to the 20 mag per arcsec2 isophotal radius under
typical observing conditions. The minimum radius is set at
R=7´´, due to the rapidly increasing (PSF shape and
background noise) uncertainty in the isophotal or Kron radial measurement for
radii smaller than this limit.
For purposes of computing colors, two classes of adaptive photometry are
carried out: individual and fiducial. "Individual" photometry refers to
the use of adapted apertures derived per band, which is useful for single-band
limited studies. The 2MASS database names (semi-major axis radius, integrated
flux, uncertainty and confusion flag) for individual Kron photometry are
"<band>_r_e",
"<band>_m_e",
"<band>_msig_e", and
"<band>_flg_e", for elliptical apertures, and
"<band>_r_c",
"<band>_m_c",
"<band>_msig_c", and
"<band>_flg_c", for circular apertures.
Database names for individual 20 mag per arcsec2
isophotal photometry are
"<band>_r_i20e",
"<band>_m_i20e",
"<band>_msig_i20e", and
"<band>_flg_i20e", for elliptical apertures, and
"<band>_r_i20c",
"<band>_m_i20c",
"<band>_msig_i20c", and
"<band>_flg_i20c", for circular apertures.
Individual 21 mag per arcsec2 isophotal photometry names are
"<band>_r_i21e",
"<band>_m_i21e",
"<band>_msig_i21e", and
"<band>_flg_i21e", for elliptical apertures, and
"<band>_r_i21c",
"<band>_m_i21c",
"<band>_msig_i21c", and
"<band>_flg_i21c", for circular apertures.
The real power of 2MASS data is having simultaneous J-Ks, J-H
and H-Ks colors. Colors require a consistent aperture size
and shape for all three bands, based on either the J or Ks
isophotes, respectively referred to as the "J fiducial" and "K fiducial"
photometry. For the brighter galaxies in the catalog, Ks <
13 mag, the "K" fiducial isophotal elliptical aperture photometry
appears to give the most precise measurement (based on repeatability tests),
but errors in the ellipse fit to the 3
Additional flux measures include the central surface brightness (peak pixel
flux) and the "core" surface brightness (average flux over a 5´´
radius). Database names are
"<band>_peak" and
"<band>_5surf",
for the peak and core surface brightness respectively.
Finally, a "system" measurement is carried out in which no stellar masking is
performed, nor any masking of flux from neighboring galaxies. The "system"
flux indicates the total flux in and about a galaxy, so it will include the
total light in closely interacting systems. A set of contamination flags
supplement the system measurements: one indicating stellar contamination and
the other neighboring galaxy "contamination." Database names are
"<band>_m_sys",
"<band>_msig_sys" and
"sys_flg", for the integrated flux, uncertainty and confusion flag,
respectively.
The extrapolation mags represent the "total" flux of the object.
The (circularly-shaped) radial surface brightness profile
is first fit with a two-parameter exponential function, deriving the scale
length
 ). The precise isophote value is derived from
preset surface brightness values, one for each band, that are chosen to match
(in a statistical sense) an equivalent surface brightness of ~3
). The precise isophote value is derived from
preset surface brightness values, one for each band, that are chosen to match
(in a statistical sense) an equivalent surface brightness of ~3 . These values are 20.09 mag/arcsec2 at
J, ~19.34 mag/arcsec2 at H and ~18.55 mag/arcsec2 at
Ks, each corresponding to about ~3
. These values are 20.09 mag/arcsec2 at
J, ~19.34 mag/arcsec2 at H and ~18.55 mag/arcsec2 at
Ks, each corresponding to about ~3 for typical background levels encountered in 2MASS. The isophote center is
anchored to the intensity peak-pixel of the source, where no attempt is made
to iteratively adjust the isophote central position. The resultant elliptical
parameters, axis ratio (b/a) and position angle
(
for typical background levels encountered in 2MASS. The isophote center is
anchored to the intensity peak-pixel of the source, where no attempt is made
to iteratively adjust the isophote central position. The resultant elliptical
parameters, axis ratio (b/a) and position angle
( ), are meant to
represent the object orientation. It is this orientation that is used
as a template for elliptical-isophotal and Kron photometry (described
below) and for symmetry parameterization (also described
below).
), are meant to
represent the object orientation. It is this orientation that is used
as a template for elliptical-isophotal and Kron photometry (described
below) and for symmetry parameterization (also described
below).
 isophote (note: a real "limb" associated
with the galaxy will generally be wider than 1 pixel). Moreover, since the
desired ellipse model is symmetric across the major and minor axes, it tends
to minimize the effects of asymmetric features (such as the presence of a
nearby source). A "clean" isophote is critical for reliable convergence to the
actual object orientation.
isophote (note: a real "limb" associated
with the galaxy will generally be wider than 1 pixel). Moreover, since the
desired ellipse model is symmetric across the major and minor axes, it tends
to minimize the effects of asymmetric features (such as the presence of a
nearby source). A "clean" isophote is critical for reliable convergence to the
actual object orientation.
 isophote belonging
to the objective galaxy, it is a straightforward procedure to fit an ellipse
to the data. We assume that the center of the isophote corresponds to the peak
in the light distribution (i.e., the peak pixel). The desired ellipse is then
fully described by the axis ratio, position angle and Ks-band
semi-major radius. The identifier names in the 2MASS database are
"<band>_ba", "<band>_phi", and
"r_3sig", respectively. We derive these values by minimizing the
function
isophote belonging
to the objective galaxy, it is a straightforward procedure to fit an ellipse
to the data. We assume that the center of the isophote corresponds to the peak
in the light distribution (i.e., the peak pixel). The desired ellipse is then
fully described by the axis ratio, position angle and Ks-band
semi-major radius. The identifier names in the 2MASS database are
"<band>_ba", "<band>_phi", and
"r_3sig", respectively. We derive these values by minimizing the
function
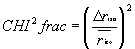

(Eq. IV.5.1)
which describes the elliptical radial distribution of the
3 isophote given some
(b/a,
isophote given some
(b/a,  ) solution.
If rijiso refers to the semi-major
radius corresponding to 3
) solution.
If rijiso refers to the semi-major
radius corresponding to 3 isophote
(i, j) pixel located (
isophote
(i, j) pixel located ( x,
x,
 y) from
the central peak pixel position, then the mean radial distribution of
3
y) from
the central peak pixel position, then the mean radial distribution of
3 isophote pixels is
isophote pixels is 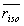 and the population standard deviation is
and the population standard deviation is
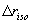 . If the ellipse
(oriented by b/a and
. If the ellipse
(oriented by b/a and  ) is perfectly
matched to the isophote, then the mean variance in riso is
identically zero, and
) is perfectly
matched to the isophote, then the mean variance in riso is
identically zero, and 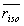 represents the ellipse semi-major axis,
rsemi. But if the match is poor, then the variance is large,
while the population mean can be large or small, generally resulting in a
large
represents the ellipse semi-major axis,
rsemi. But if the match is poor, then the variance is large,
while the population mean can be large or small, generally resulting in a
large  2 value. Therefore, by
minimizing the ratio of the standard deviation to the mean radius in
the distribution, we arrive at the best-fit ellipse solution. In this fashion,
the elliptical parameters are derived for each band. Due to the resolution and
sensitivity of the survey, there are practical limits to which we can measure
the orientation and size of a galaxy: the minimum axis ratio is floored at
0.10 and the minimum semi-major axis radius is 5.0´´ (see below).
We will refer to Eq. IV.5.1 as the "goodness of fit" or "chi-frac" metric; the
J and Ks-band database names are "j_chi_ellf" and
"k_chi_ellf", respectively. The goodness of fit
metric can used to indicate problems with the fit (due to stellar contamination
or noise in the case of faint sources) or real asymmetry in the object.
2 value. Therefore, by
minimizing the ratio of the standard deviation to the mean radius in
the distribution, we arrive at the best-fit ellipse solution. In this fashion,
the elliptical parameters are derived for each band. Due to the resolution and
sensitivity of the survey, there are practical limits to which we can measure
the orientation and size of a galaxy: the minimum axis ratio is floored at
0.10 and the minimum semi-major axis radius is 5.0´´ (see below).
We will refer to Eq. IV.5.1 as the "goodness of fit" or "chi-frac" metric; the
J and Ks-band database names are "j_chi_ellf" and
"k_chi_ellf", respectively. The goodness of fit
metric can used to indicate problems with the fit (due to stellar contamination
or noise in the case of faint sources) or real asymmetry in the object.
 ) replaces the given masked pixel that the
isophote passes through. More detailed discussion of stellar contamination and
rectification thereof in 2MASS galaxy photometry can be found in Jarrett et
al. (1996, in The Impact of Large Scale Near-IR Sky Surveys, p. 213).
) replaces the given masked pixel that the
isophote passes through. More detailed discussion of stellar contamination and
rectification thereof in 2MASS galaxy photometry can be found in Jarrett et
al. (1996, in The Impact of Large Scale Near-IR Sky Surveys, p. 213).
 isophote
(see previous subsection) result in an uncertainty that
is difficult to evaluate (see Appendix A). The
adaptive circular apertures reduce some of that
uncertainty, but do increase the overall noise, due to additional sky noise
within the non-optimized aperture-resulting in a less precise, but more robust
measurement. 2MASS database names (semi-major axis radius, integrated flux,
uncertainty and confusion flag, respectively) for fiducial Kron photometry are
"r_fe",
"<band>_m_fe",
"<band>_msig_fe", and
"<band>_flg_fe", for elliptical apertures, and
"r_fc",
"<band>_m_fc",
"<band>_msig_fc", and
"<band>_flg_fc", for circular apertures.
Database names for fiducial 20 mag per arcsec2 isophotal photometry
are
"r_k20fe",
"<band>_m_k20fe",
"<band>_msig_k20fe", and
"<band>_flg_k20fe", for elliptical apertures, and
"r_k20fc",
"<band>_m_k20fc",
"<band>_msig_k20fc", and
"<band>_flg_k20fc", for circular apertures.
J-band fiducial 21 mag per arcsec2 isophotal photometry names are
"r_j21fe",
"<band>_m_j21fe",
"<band>_msig_j21fe", and
"<band>_flg_j21fe", for elliptical apertures, and
"r_j21fc",
"<band>_m_j21fc",
"<band>_msig_j21fc", and
"<band>_flg_j21fc", for circular apertures.
isophote
(see previous subsection) result in an uncertainty that
is difficult to evaluate (see Appendix A). The
adaptive circular apertures reduce some of that
uncertainty, but do increase the overall noise, due to additional sky noise
within the non-optimized aperture-resulting in a less precise, but more robust
measurement. 2MASS database names (semi-major axis radius, integrated flux,
uncertainty and confusion flag, respectively) for fiducial Kron photometry are
"r_fe",
"<band>_m_fe",
"<band>_msig_fe", and
"<band>_flg_fe", for elliptical apertures, and
"r_fc",
"<band>_m_fc",
"<band>_msig_fc", and
"<band>_flg_fc", for circular apertures.
Database names for fiducial 20 mag per arcsec2 isophotal photometry
are
"r_k20fe",
"<band>_m_k20fe",
"<band>_msig_k20fe", and
"<band>_flg_k20fe", for elliptical apertures, and
"r_k20fc",
"<band>_m_k20fc",
"<band>_msig_k20fc", and
"<band>_flg_k20fc", for circular apertures.
J-band fiducial 21 mag per arcsec2 isophotal photometry names are
"r_j21fe",
"<band>_m_j21fe",
"<band>_msig_j21fe", and
"<band>_flg_j21fe", for elliptical apertures, and
"r_j21fc",
"<band>_m_j21fc",
"<band>_msig_j21fc", and
"<band>_flg_j21fc", for circular apertures.
 and modifier
and modifier
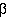 ,
according to Eq. IV.5.2 (below).
The profile extends down to the 20 mag arcsec-2
isophote (per band). The inner 10´´ radius is excluded from the fit
due to the proximal effects of the PSF (hence, f0 is set to
the isophotal value at 10´´ radius). The exponential is then
extrapolated from the Kron radius (R<band>c,
corresponding to 2.5 times the first moment radius),
down to four times the Kron radius, with a maximum of 80´´ in radius.
,
according to Eq. IV.5.2 (below).
The profile extends down to the 20 mag arcsec-2
isophote (per band). The inner 10´´ radius is excluded from the fit
due to the proximal effects of the PSF (hence, f0 is set to
the isophotal value at 10´´ radius). The exponential is then
extrapolated from the Kron radius (R<band>c,
corresponding to 2.5 times the first moment radius),
down to four times the Kron radius, with a maximum of 80´´ in radius.
| RJext | J extrapolation radius |
| Jext | J mag from fit extrapolation |
| RHext | H extrapolation radius |
| Hext | H mag from fit extrapolation |
| RKsext | Ks extrapolation radius |
| Ksext | Ks mag from fit extrapolation |
The utility of the extrapolation mags is limited to galaxies larger than 10´´, but smaller than 80´´. For this size range, the average mag offset between the circular isophotal mags (20 mag arcsec-2) and the extrapolated mags is 0.33 ± 0.12 (band independent). In other words, the extrapolated mags recover 30% of the flux that is "lost" in the noise. One should cautiously keep in mind that the actual offset is morphology-dependent.
A cautionary note: like all isophotes used in 2MASS pipeline processing,
the magnitudes of the isophotal contour for the isophotal magnitude are
uncalibrated to 10%-20% and may be adjusted by ~0.1 to 0.2 mag in the later
calibration processing step. Consequently, the isophote at which the
2-D elliptical parameters are derived can vary from (in background noise units)
~2.6 - 3.7
- 3.7 ,
depending on the calibration correction.
,
depending on the calibration correction.
v. Source Parameterization
The first step toward discerning extended sources, including galaxies and
Galactic nebulae, from point sources (mostly stars) is to characterize the
point spread function accurately. The distinctive shape of the 2MASS PSF
derives from a combination of factors: the optics, large 2´´ pixels
(frame images), dithering pattern of the six frame samples that comprise the
Atlas image, location of the source within the unit cell of dither pattern,
focus, sampling/convolution algorithm to generate the Atlas images, and
atmospheric seeing. As such, the 2MASS PSF corresponding to frame-coadded
images is not well fit with a simple Gaussian function. It can, however, be
adequately characterized by a generalized exponential function (see below) out
to a radius ~2×FWHM, that makes effective star-galaxy discrimination
possible.
The 2MASS PSF typically varies on time scales of ~minutes due to:
atmospheric "seeing" and thermally-driven variable telescope focus. The 2MASS
telescopes are designed to be mostly free of afocal PSFs (under most
conditions), but 2MASS images can be slightly out of focus during periods of
rapid change in the air temperature - conditions that generally only occur
during the hottest summer months. Out-of-focus images have the difficult
property of possessing elongated PSFs. Fortunately, under most typical
observing conditions for the survey, the PSFs are symmetric throughout the
focal plane. That leaves the atmospheric seeing as the primary dynamic to the
radial size of the PSF. Given the exposure times per sample (1.3 s) and the
six-sample co-addition (with optimal dithering to produce round PSFs), seeing
changes result in a mostly symmetric "puffing" in and out of the resultant
Atlas image PSF (the seeing "speckle" pattern is negligible given the 1.3-s
exposure time per frame and the co-addition smoothing). We can represent the
image PSF with the generalized radially symmetric exponential of the form:
where f0 is the central surface brightness, r is
the radius in arcsec, and
Although the generalized surface brightness function (Eq. IV.5.2) can be used
to derive meaningful fit parameters for galaxies brighter than Ks ~
12 mag, for fainter galaxies the fit parameters are heavily
influenced by the PSF and image noise. Furthermore, due to the relatively
small areal region of the fit (Eq. IV.5.2) to the radial surface brightness,
typically only ~8´´ in radius to minimize the
effects of background noise, scale-length
The "shape" is also used as the atmospheric "seeing" metric for 2MASS point
and extended source data. The generalized exponential function (Eq. IV.5.2) is
applied to all sources, and a robust "shape" value is derived from an interval
of time by careful analysis (see below). Here the "shape" is analogous to a
FWHM measurement for the time-variable PSF. Our ability to track the seeing on
short time scales depends on the density of stars. The more stars available
to measure a statistically meaningful value of the "shape," the higher the
frequency of seeing changes that can be tracked. A reasonable shape value can
be derived from a minimum of about 10 stars. Consequently, for low
stellar-density regions, like the north Galactic pole (~300 stars per
deg2 brighter than 14 mag at 2.2µm) the seeing is tracked on
time scales of about 30 s;
for high density regions (>104 stars deg-2) is
tracked on time scales of a few seconds. Experience has shown that the seeing
can indeed significantly change on times scales as fast as seconds of time
(see below).
As is the case for all ground based observations, the PSF changes with time
due to the changing thermal environment and dynamic atmospheric "seeing". The
stellar "ridgeline" refers to the mean values of the PSF "shape" during an
observation scan (6° in length and about 6
minutes of real time). The stellar ridgeline provide two important pieces of
information crucial to both "seeing" tracking and star-galaxy separation: (1)
time-dependent PSF, and (2) the uncertainty or spread in the stellar PSF
distribution. The spread is a combination of an intrinsic component arising
from the pixel undersampling in the original frames and dither pattern for
co-addition, and an environmental component-the short time interval from which
the main "shape" is computed is subject to small but variable seeing and focus
changes.
The mean "shape" is determined from an ensemble of isolated stars spatially
clustered along the in-scan direction (the arrow of time). The sample
population must be free of extended sources (galaxies) and double stars to be
a meaningful measure of the PSF. We employ an iterative selection method that
is keyed by using an initial boot-strap from the lower quartile of the
total population histogram. Since isolated stars will have an inherently
smaller "shape" value than extended sources (or double stars), the lower
quartile (25%) is populated nearly entirely by isolated stars and the upper
quartile will be contaminated by resolved sources such as double stars and
galaxies. Hence, the distribution's lower quartile serves as a good first
guess to the actual mean shape value of isolated stars. Once the lower
quartile is identified, we can iteratively search a restricted range in the
histogram to arrive at a stable and robust estimation of the true mean shape
value for isolated stars. The initial restricted range corresponds
-3
For the time-variable "seeing", we use the ridgeline to characterize the
radial extent of the PSF. Two very different examples are illustrated in
Figures 5 and
6. The plots show the median "shape" values
(large filled circles) along the scan. Extracted sources (including stars and
galaxies) are denoted with small points. The approximate (Gaussian derived)
FWHM of the PSF are also shown to give some idea of the angular scale in
arcseconds and the approximate relation between
Extended sources lie above the ridgeline defined by stars. We can reliably
begin to separate stars from resolved sources at ~2 to 3 times the spread in
the "shape" ridgeline. More generally, we can assess the "extendedness" of a
source by how far it lies from the stellar ridgeline. The radial "shape"
(
where SH0 (t´) and
The SH uncertainty includes both measurement
error and the intrinsic PSF spread. However, since SNR > 10 stars are
plentiful in most areas, the measurement error is minimal compared to the real
spread in the PSF. The uncertainty represents the RMS in the SH
distribution, but the distribution has
triangular-shaped wings (i.e., the scatter in SH falls off linearly),
due to the undersampling (in the original frames)
and sub-pixel dither to optimally coadd the frames into Atlas Images.
Consequently, stars will not have SH values above
a threshold of ~2·
Characterizing the Point Spread Function
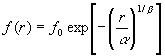

(Eq. IV.5.2)
 and
and
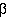 are
free parameters. This versatile function (cf. Sersic 1968), not only describes
the 2MASS PSF, but it is also used to characterize the radial profiles of
galaxies, from disk-dominated spirals (
are
free parameters. This versatile function (cf. Sersic 1968), not only describes
the 2MASS PSF, but it is also used to characterize the radial profiles of
galaxies, from disk-dominated spirals (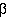 close to
unity) to ellipsoidal galaxies (
close to
unity) to ellipsoidal galaxies (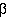 ~ 4, de
Vaucouleurs "law"). It has even been used to describe less-defined
morphologies: Binggeli & Jerjen (1998, A&A, 333, 17)
successfully modeled the surface
brightness profiles of cD and dwarf spheroidal galaxies with this method.
~ 4, de
Vaucouleurs "law"). It has even been used to describe less-defined
morphologies: Binggeli & Jerjen (1998, A&A, 333, 17)
successfully modeled the surface
brightness profiles of cD and dwarf spheroidal galaxies with this method.
The Radial "Shape" of Galaxies and Stars
 and
modifier
and
modifier 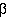 exhibit a high degree of correlation,
and hence individual values of these parameters are not meaningful or
physically connected to the source itself. Nevertheless, the fit parameters
have still proved useful to distinguish extended sources from point sources.
In particular, the quantity
(
exhibit a high degree of correlation,
and hence individual values of these parameters are not meaningful or
physically connected to the source itself. Nevertheless, the fit parameters
have still proved useful to distinguish extended sources from point sources.
In particular, the quantity
( ×
×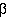 ) robustly
measures the average spatial extent of a source. Resolved galaxies tend to
have larger values of both
) robustly
measures the average spatial extent of a source. Resolved galaxies tend to
have larger values of both  and
and
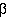 than stars, so the
multiplicative join of the
exponential fitting parameters amplifies the difference between point sources
and extended sources. The (
than stars, so the
multiplicative join of the
exponential fitting parameters amplifies the difference between point sources
and extended sources. The ( ×
×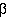 ) quantity, referred to
as the "radial shape" (or in short, "shape"), is the fundamental parameter for
distinguishing between isolated stars and resolved objects (e.g., galaxies).
Its variant cousins (described in the next subsection) provide further power for
discriminating galaxies from more complex point sources, including double and
triple stars.
) quantity, referred to
as the "radial shape" (or in short, "shape"), is the fundamental parameter for
distinguishing between isolated stars and resolved objects (e.g., galaxies).
Its variant cousins (described in the next subsection) provide further power for
discriminating galaxies from more complex point sources, including double and
triple stars.
Stellar Ridgelines and Tracking the PSF
 to +2
to +2 of
the lower quartile, where
of
the lower quartile, where  is the RMS scatter
in the "shape" value.
In the first iteration we use an a priori determination of
is the RMS scatter
in the "shape" value.
In the first iteration we use an a priori determination of
 . For each iteration thereafter, we set hard
limits of ±2
. For each iteration thereafter, we set hard
limits of ±2 . The final
"shape" value corresponds to the median (50% central quartile) of the
restricted histogram sample, and the
. The final
"shape" value corresponds to the median (50% central quartile) of the
restricted histogram sample, and the  to the
RMS scatter or standard deviation of the population. The 2MASS database names
are "<band>_sh0" and "<band>_sig_sh0", respectively.
to the
RMS scatter or standard deviation of the population. The 2MASS database names
are "<band>_sh0" and "<band>_sig_sh0", respectively.
 ×
×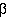 "shape" and the more standard PSF FWHM. Note that these two measures are not
uniquely related, but instead provide a more
general relationship. In Figure 5 we show
the resultant ridgeline for a scan
passing through the Hercules cluster of galaxies. The stellar number density
is not large (Galactic latitude of Hercules is about 30°), but there are
still plenty of isolated stars
easily separated from the cluster sources which are located above the mean
"shape" ridge of stars. The seeing is fairly stable for each band all
throughout the 6° scan spanning ~6 minutes of time. The same cannot be
said for the second case, Figure 6, which
demonstrates
both poor seeing conditions and very rapid changes in the PSF. Fortunately,
the stellar density is relatively high in this field, ~4000 stars per
deg2, and the rapid seeing diversions are, for the most part,
sufficiently tracked. Scans for which the seeing is poorly tracked or the
absolute value of the mean scan seeing is greater than 1.3´´
(~PSF FWHM > 4´´)
are considered low quality data and are in most cases scheduled for
re-observation.
"shape" and the more standard PSF FWHM. Note that these two measures are not
uniquely related, but instead provide a more
general relationship. In Figure 5 we show
the resultant ridgeline for a scan
passing through the Hercules cluster of galaxies. The stellar number density
is not large (Galactic latitude of Hercules is about 30°), but there are
still plenty of isolated stars
easily separated from the cluster sources which are located above the mean
"shape" ridge of stars. The seeing is fairly stable for each band all
throughout the 6° scan spanning ~6 minutes of time. The same cannot be
said for the second case, Figure 6, which
demonstrates
both poor seeing conditions and very rapid changes in the PSF. Fortunately,
the stellar density is relatively high in this field, ~4000 stars per
deg2, and the rapid seeing diversions are, for the most part,
sufficiently tracked. Scans for which the seeing is poorly tracked or the
absolute value of the mean scan seeing is greater than 1.3´´
(~PSF FWHM > 4´´)
are considered low quality data and are in most cases scheduled for
re-observation.
 ×
×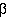 ), or simply
SH, of a source is compared to the stellar ridge value,
SH0 , and an N-
), or simply
SH, of a source is compared to the stellar ridge value,
SH0 , and an N- "score" is
computed as:
"score" is
computed as:
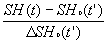

(Eq. IV.5.3)
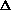 SH0 (t´)
denote the time variable ridgeline value and its associated uncertainty and
SH(t), the
source value, with time t´ as close to real t as
possible. The PSF ridgeline value is stable over all flux levels, so only one
value is needed per time interval. The 2MASS database name for the
SH "score"
parameter is "<band>_sc_sh".
SH0 (t´)
denote the time variable ridgeline value and its associated uncertainty and
SH(t), the
source value, with time t´ as close to real t as
possible. The PSF ridgeline value is stable over all flux levels, so only one
value is needed per time interval. The 2MASS database name for the
SH "score"
parameter is "<band>_sc_sh".
 SH0,
but galaxies and other relatively
"extended" objects (e.g., double stars) will have scores >2. In the
following subsections we will describe how we separate real extended sources
(e.g., galaxies) from false extended sources (e.g., double stars) using
several different flavors of stellar ridgelines.
SH0,
but galaxies and other relatively
"extended" objects (e.g., double stars) will have scores >2. In the
following subsections we will describe how we separate real extended sources
(e.g., galaxies) from false extended sources (e.g., double stars) using
several different flavors of stellar ridgelines.
|
 |
| Figure 5 | Figure 6 |
vi. Star - Galaxy Discrimination
The ability to separate real extended sources (e.g., galaxies, nebulae, H II
regions, etc.) from the vastly more numerous stars detected by 2MASS is what
fundamentally limits the reliability of any extended source catalog. Single
isolated point sources represent the purest and easiest construct from which
extended sources must be distinguished. More complicated constructs include
"double" stars and "triple+" stars, these are generic labels that include both
physically-associated multiple systems and (more likely) chance superposition
of stars on the sky. The permutations and combinations of multiple-star
characteristics (radial separation, flux difference, color difference, etc.)
make them a challenge to separate from real galaxies. The surface density of
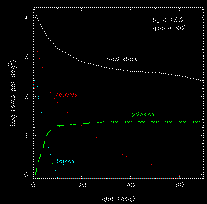
stars and galaxies is illustrated in Figure
7. Double stars are less than ~2% of
the total stellar count at high Galactic latitudes, but begin to dominate the
total numbers for |b| < 5°. Even at moderate
stellar number density, double stars are comparable in number to galaxies for
typical 2MASS flux levels.
There are many competing methods for separating stars from galaxies (or more
generally, "classification"), from the simplest classification and regression
tree methods (CART; e.g., linearly measuring one attribute vs. another), to
Early experimentation with existing algorithms (e.g., FOCAS) were
unsatisfactory due primarily to the severely undersampled 2MASS PSF, which
changes over time scales of minutes. A critical issue for GALWORKS is
to accurately measure and track the time-varying PSF (see
above) while
applying some simple CART-like rules to cull out most of the multiple stars
and artifacts that mimic real extended sources. The resultant extended source
database is approximately 80% reliable for most of the sky. In a
post-processing phase, further refinements, including more complicated
attribute combinations and decisions trees (see
below), are used to produce the
extended source catalog at a reliability of greater than 98% for Ks
< 13.5 mag. Later we describe and discuss some of the more critical
parametric measurements and decision tree operations utilized to that end.
 2 automated induction (CHAID), to the
more sophisticated Bayesian-based methods (e.g., FOCAS; see Valdes 1982,
SPIE Proc. On Instrumentation in Astronomy IV, 331, 465),
decision trees (e.g., Weir, Fayyad & Djorgovski, 1995, AJ, 109, 2401)
and neural networks (e.g., Odewahn et al. 1992, AJ, 103, 318; Bertin &
Arnouts 1996, A&AS, 117, 393). Each method was
designed in response to increasingly more complicated data sets. For 2MASS, we
were faced with undersampled near-infrared images subject to a variable PSF
shape that called for a special adaptation of these procedures.
2 automated induction (CHAID), to the
more sophisticated Bayesian-based methods (e.g., FOCAS; see Valdes 1982,
SPIE Proc. On Instrumentation in Astronomy IV, 331, 465),
decision trees (e.g., Weir, Fayyad & Djorgovski, 1995, AJ, 109, 2401)
and neural networks (e.g., Odewahn et al. 1992, AJ, 103, 318; Bertin &
Arnouts 1996, A&AS, 117, 393). Each method was
designed in response to increasingly more complicated data sets. For 2MASS, we
were faced with undersampled near-infrared images subject to a variable PSF
shape that called for a special adaptation of these procedures.
 |
| Figure 7 |
Basic Object Characteristics
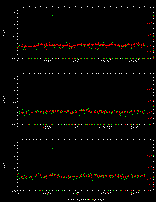
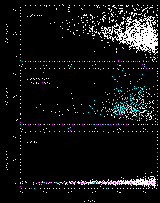
The shape parameter is an effective star-galaxy discriminator: isolated stars and "resolved" sources (e.g. galaxies, double stars) are differentiated. In Figure 8 we display the J-band SH scores of three kinds of objects that 2MASS commonly encounters: stars, multiple stars (double stars and triple+ stars), and galaxies. Stars occupy a locus about zero SH score (as a result of defining the stellar ridgeline), while multiple stars lie well above the ridgeline along with galaxies and other "fuzzy" sources. The number of stars displayed has been reduced by a factor of 10 relative to the other plots in order to show the scatter in shape for the ridgeline vs. magnitude. The SH score is very effective at separating isolated stars from galaxies at flux levels as faint as J~15.4 mag.
Other GALWORKS-derived image parameters that are also effective at separating isolated stars from extended sources include the first and second intensity-weighted moments (2MASS database name are "<band>_sc_1mm" and "<band>_sc_2mm", respectively), ratio of the central surface brightness to the integrated brightness ("<band>_sc_mxdn"), and differential areal measures (e.g., isophotal area; "<band>_d_area"). Unfortunately, like the radial SH parameter, none of these diagnostics can discriminate galaxies from sky-projected clusters (i.e., double and triple+ stars) to the degree necessary to meet the Level 1 requirements. Double stars are particularly vexing due to their sheer numbers at |b| < 20° (Figure 7). Double stars (and triple stars near the Galactic plane) are clearly the primary contaminant of the galaxy database. More intricate attributes are needed to exploit the differences between groupings of point sources and genuinely extended sources.
 |
| Figure 8 |
In the near-infrared, the observed morphology for galaxies usually has smooth
radial and azimuthal profiles. Spiral galaxies have much more even light
distributions in the near-infrared than optical because the absorption is
greatly reduced and the emission is dominated by older stellar populations,
including low mass dwarfs and red giants, which are less concentrated in spiral
arms. Features commonly seen at the radio and optical wavelengths, including
H II regions, supernova remnants and dust lanes, are generally difficult to
detect in the near-infrared except in the nearest galaxies;
Figure 9 shows a few
large angular scale galaxies located in the Virgo cluster. Only the relatively
rare cases of galaxies subject to strong tidal or hydrodynamical interactions
exhibit significant asymmetry in the near-infrared bands.
In contrast, multiple stars, and in particular double stars, are not
radially symmetric about their "primary" peak-pixel center. Here the primary
center of light of a multiple star corresponds to the brightest member in the
group, or more specifically, the peak pixel associated with the brightest star,
but can be in between for pairs of stars of equal brightness. We should point
out an important feature of GALWORKS: it does not
assume that a resolved object (i.e., two or more detections in close proximity)
is a double or triple star, since real galaxies may be also be
multiply-detected (in particular, bright edge-on galaxies may induce several
detections along its disk). Hence, we do not make a distinction between double
stars that are resolved or unresolved with respect to the PSF. Instead, we
must apply other tests to decide whether an object is truly "extended" or not.
Below we describe the methods that are utilized in the pipeline
GALWORKS software.
The near-infrared symmetry of galaxies can be exploited to differentiate
between multiple stars that otherwise mimic extended sources.
Figure 10
illustrates a variety of double stars seen in 2MASS images. For comparison, a
set of galaxies of approximately the same integrated brightness as that of the
double stars is also shown in the lower panels. Both sets of sources were
classified using higher resolution (~1´´ PSF)
optical imaging data and with the Digitized Sky Survey image data (see also
below for a description of the "training sets").
Surface brightness
profiles and colors distinguish true extended sources from point-like objects
(in this case, double stars). For double stars, the fainter star ("secondary"
component) breaks the symmetry about the primary. Hence, the signature of a
double star is an asymmetric azimuthal profile.
Multiple Star - Galaxy Separation using Symmetry Metrics

|
 |
| Figure 9 | Figure 10 |
So as not to enforce a strong bias against asymmetric or foreground-contaminated galaxies, the various "symmetry" parameters and metrics used to discriminate galaxies from stars (described below) are used judiciously in conjunction with non-biased parameters (e.g., SH). Here we employ two different strategies at forming symmetry parameters. The first is to exploit the measured 2-dimensional orientation of the source, and the second is to utilize the generalized PSF function (Eq. IV.5.2) under scenarios in which the degree of asymmetry in the object can be measured.
Once the general orientation of the galaxy is derived (see
above),
the "symmetry" of the object can be appraised. As discussed earlier, the
radial and azimuthal symmetry of an object is a good indicator of its true
nature. Double stars appear asymmetric across the minor axis-since the ellipse
is centered on the primary component of the double star. This is also
generally the case for triple stars, although there are maddening
configurations of  3 stars in which the
alignment is symmetric across both the minor and major axes.
3 stars in which the
alignment is symmetric across both the minor and major axes.
One way to measure the "symmetry" of an object is to perform a bi-symmetric
flux comparison between the two half-sides as defined by the minor axis (see
above). Perfectly symmetric objects will have a flux
ratio that is equal to
unity. We may also cross-correlate the pixel-values in the two halves by
simply rotating one side 180° with respect to the other and multiply
the resultant pieces. The desired asymmetry "measure" is then the sum,
normalized by the total integrated flux squared. To minimize the effects of
noise and the shape of the PSF, very low SNR points (< 1.5) and the inner
3´´ core are avoided in this procedure. A more
elegant variation on this method avoids the deleterious effects of low SNR
points; namely, we perform the cross-correlation with a reduced
 2
function of the form,
2
function of the form,
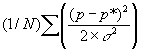 |
 |
(Eq. IV.5.4) |
where p and p* are pixel values at points 180° apart,
N is the number of points being compared, and
 is the pixel noise
(but ignoring the noise contribution of photons from the source itself). This
is the pixel noise
(but ignoring the noise contribution of photons from the source itself). This
 2 measure has the multiple advantage
that it has a distribution that is well understood statistically with tabulated
confidence ranges, there are no asymmetries in the distribution like those
introduced in a ratio comparison, and it is insensitive to low SNR or data
points near zero. The final symmetry measure comes from the object orientation
"goodness of fit" parameter (Eq. IV.5.1). The 2MASS database names are
"<band>_bisym_rat",
"<band>_bisym_chi"
and "<band>_chif_ellf", for the bi-symmetry flux ratio,
cross-correlation and ellipse "goodness of fit" to the
3-
2 measure has the multiple advantage
that it has a distribution that is well understood statistically with tabulated
confidence ranges, there are no asymmetries in the distribution like those
introduced in a ratio comparison, and it is insensitive to low SNR or data
points near zero. The final symmetry measure comes from the object orientation
"goodness of fit" parameter (Eq. IV.5.1). The 2MASS database names are
"<band>_bisym_rat",
"<band>_bisym_chi"
and "<band>_chif_ellf", for the bi-symmetry flux ratio,
cross-correlation and ellipse "goodness of fit" to the
3- isophote, respectively.
isophote, respectively.
A different tactic is to "remove" the secondary and measure the resultant
SH (Eq. IV.5.3) of the "deblended" primary. We are, of
course, faced with the problem that the emission from both sources are
entangled and the primary itself has changed both its radial (SH) width
and its azimuthal (symmetry) shape. If the
PSFs were exceptionally stable and well characterized as such, then in
principle it would be possible to satisfactorily de-blend the multiple sources
into their constituent parts. Since this condition is not always realized, and
moreover the runtime for this kind of multiple PSF
 2 fitting is prohibitively
long, we are left with less ideal methods.
2 fitting is prohibitively
long, we are left with less ideal methods.
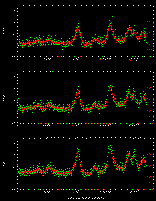
The simplest approach is to remove the secondary using a median filter in annular shells about the primary: GALWORKS refers to the resultant measure as the "median shape" or MSH (in the database it is called "<band>_sc_msh"). A more satisfactory (if more complicated) approach is to mask the secondary and measure the residual emission from the primary, using a 45° wedge or pie-shaped mask that is rotated about the vertex anchored to the primary. The optimum configuration in which the secondary is effectively masked is found by rotating the wedge mask through all angles (Figure 11). The SH score is then computed for the remaining area (360° - 45°). If the secondary star is masked, then the resultant SH score will be minimized, ideally with a value corresponding to an isolated star. In practice the secondary can never be fully masked, and the peak pixel does not represent the true center of the primary since it is slightly shifted toward the secondary-thus resulting in a slightly inflated SH score relative to that of an isolated star. Nevertheless, the "wedge" shape score, or WSH (in the database it is called "<band>_sc_wsh"), is an effective discriminant. This is demonstrated in Figure 12, which is analogous to Figure 8; here we show the distribution of multiple stars and galaxies as measured in the WSH vs. magnitude plane.
The wedge shape score for double stars is considerably smaller than the corresponding SH score, having values typically less than 5 for J < 15 mag, while galaxies remain "extended" in this measure with scores >5 for J < 15 mag. Note however, triples+ stars are only occasionally identified as such by the WSH score since the additional two secondary components usually defeat the single rotating mask method. For triple stars, yet more severe "symmetry" constraints are required.
Triple stars are geometrically more difficult to characterize because of
the number of possible combinations of integrated flux and primary-secondary
separations. For most triple stars there is minimal contamination from the two
secondary components along some radial direction from the primary. If we
measure the radial SH of this vector and compare
it to the corresponding ridgeline value, the resultant "score" should be close
to that of an isolated star. Thus the basic method is to measure the
SH along an azimuthally distributed set of vectors at
angular separations of 5°. The vector corresponding to the "minimum" shape
score (referred to as the R1 score; in the database it is called
"<band>_sc_r1") is susceptible to background noise
fluctuations since we are restricting the
( ,
,  )
fitting operation to less than a dozen pixels. For galaxies, the R1
score tends to select against galaxies that are
edge-on and thus have minimal (but still measurable) extended emission along
the minor axis (i.e., the vector corresponding to the minimum radial
SH score).
)
fitting operation to less than a dozen pixels. For galaxies, the R1
score tends to select against galaxies that are
edge-on and thus have minimal (but still measurable) extended emission along
the minor axis (i.e., the vector corresponding to the minimum radial
SH score).
A more robust parameter, but slightly less effective at removing the influence of the secondary components, is to average the second and third lowest SH value vectors. This score is referred to as the R23 shape score (in the database it is called "<band>_sc_r23"). Here we are relying upon the fact that most triple star configurations (but not all by any means) will have more than one vector that is only minimally affected by the secondary components. Galaxies, meanwhile, are generally extended in all directions, and so the R23 score is not much different from the SH score except for the faintest galaxies (J > 15, Ks > 13.75 mag) which are at the mercy of noise fluctuations.
The effectiveness of the R23 score is demonstrated in Figure 13. Here we plot the R23 vs. magnitude phase space. It can be seen that the triple stars are now well under control with minimal loss to the galaxies at J < 14 mag. For the faint magnitude bins, J > 14 mag, galaxies are not well separated from triple stars. Fortunately, triple stars are only relatively abundant when the stellar number density is very high (i.e., the Galactic plane; see Figure 7), which means that the "confusion" noise is also high (that is, the random fluctuations in the background due to faint stars; see Appendix B), rendering the sensitivity limits for galaxy detection itself from 0.5 to nearly 2 mags brighter than the high-latitude 2MASS limits. Thus, just as the problem with triple stars becomes significant, the practical detection thresholds are correspondingly decreased, the end result is that the R23 score is an effective star-galaxy discriminator for flux levels up to the detection limits. For the most extreme stellar number density cases (e.g., in the Galactic center region), >105 stars deg-2 brighter than Ks=14 mag, quadruple ++ stars become significant, at which point there is little that can be done to separate galaxies from clusters of stars.
We have developed additional parameters designed to discriminate triple stars from extended objects, including measuring the linear flux gradient along radial vectors and the integrated flux gradient along radial "column" vectors (referred to as the VINT score; in the database it is called "<band>_sc_vint"). Similar to the R1 and R23 scores, these methods rely upon the "minimum" column integrated flux or gradient in the column flux to be similar to that of isolated stars. They are not quite as effective as the SH vector scores, but since they are only slightly correlated, they can be used in combination with the other attributes when using a decision tree classifier.
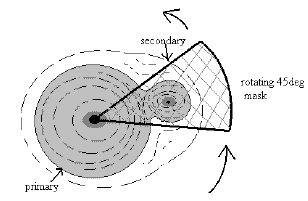
|
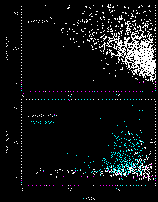
|
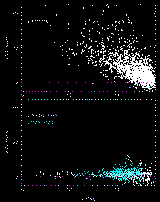 |
| Figure 11 | Figure 12 | Figure 13 |
Initial Star-Galaxy Thresholding
Preliminary flux estimates come from the point source processor, which uses a characteristic PSF to derive total fluxes (assuming a point-like flux distribution). These measures systematically underestimate the flux of extended sources. Hence, one of the first tasks for GALWORKS is to deduce the nature of a source using some simple radial profile attributes. The median radial shape score, or MSH (see previous subsection), is both quick to compute and a robust discriminator between stars/double stars and galaxies. Applying an extremely conservative threshold to the MSH measure for each source in each band separately eliminates a large fraction of the total number of sources that require more exhaustive testing for star-galaxy separation. If the source is very likely to be extended (large MSH score), then its integrated flux is re-measured using a larger circular aperture.
Before the more time-consuming image attribute measurements are performed on each source (e.g., elliptical shape fitting and adaptive aperture photometry), it is necessary to perform additional star-galaxy separation tests, particularly when the stellar number density is very high, as at |b| < 10°. Thresholds on the SH, WSH, R1, and R23 radial shape attributes (see above) are carried out to eliminate additional non-extended sources (namely stars and double stars) from the source list. For high latitude fields, the remaining sources (in a typical 6° scan) are mostly real galaxies intermixed with a few double stars, one or two isolated stars and low SNR objects of uncertain nature. The reliability is from 50 to 80% at this juncture, and thus the star-galaxy separation process has reduced the fraction of stars to galaxies from 10:1 to approximately 1:1.
vii. Post-processing Star-Galaxy Separation
The 2MASS extended source database is populated with both real extended
sources (e.g., galaxies) and with false sources (mostly double stars), as
designed in order to maximize completeness in the database at the expense of
reliability. We will construct two different kinds of catalogs: an "extended"
catalog and a galaxy catalog. The "extended" catalog is meant to be an
unbiased sample of both galaxies and Galactic sources, and is derived from the
database using simple thresholds on the SH,
WSH and R23 parameters. The
"galaxy" catalog, on the other hand, is specifically generated to produce a
reliable and complete set of galaxies. But, in order to construct a reliable
catalog of extended sources from this database, it is necessary to
perform further star-galaxy discrimination tests; namely, the color attribute
and decision tree classifier, discussed below. We should point out that even
though the galaxy catalog is composed mostly of extragalactic objects,
it will also include Galactic extended sources. We emphasize that the
procedures described in this subsection are performed after the
standard pipeline reductions: their purpose is to generate a reliable catalog
from the database of sources extracted in the standard pipeline.
Two effects make galaxies appear "red" in the 1 to 2µm window: their
light is dominated by older and redder
stellar populations (e.g., K and M giants), and their redshift tends to
transfer additional stellar light into the 2µm
window (for z < 0.5), boosting the Ks-band flux relative to the
J-band flux. The latter phenomenon is often called the "K correction,"
although the "K" here is unrelated to the infrared atmospheric-window band.
Because of this, the J-Ks color attribute can be used in
conjunction with color-independent discriminants, like the WSH
score to cleanly separate extragalactic objects
from stars. As a bonus, the color separation is enhanced in the Galactic plane
where double and triple star contamination is severe. This is because
galaxies are subject to a larger dust column compared to field stars along the
same line of sight. In Figure 14
we demonstrate the effectiveness of the
J-Ks color to separate stars from resolved galaxies in a diverse
set of fields, including areas well above the Galactic plane, referred to as
low stellar density fields (<103.1 stars deg-2
brighter than Ks=14 mag), areas closer to the plane
(|b| > 5°), referred to as moderate density fields (<103.6
stars deg-2), and finally areas in the Galactic plane in
which the stellar number density is very high (>103.6 stars per
deg2 brighter than Ks=14 mag). For the
latter case, the differential confusion noise is typically very high
(equivalent to ~1 mag in surface brightness) so the sensitivity limits
have been decreased accordingly (note: the differential confusion noise refers
to the effective loss in surface brightness sensitivity, relative to the
Galactic pole, due to stellar confusion noise, expressed in mag units; see
Appendix B for details).
A J-Ks color of ~1.0 mag appears to be a reasonable compromise for
separating stars from galaxies. For flux levels relevant to the 2MASS Level 1
specifications, Ks < 13.5 mag, a J-Ks color limit of 1.0 mag
eliminates nearly all (>95%) double stars that mimic galaxies, while more
than 90% of the total galaxy distribution has a color greater than this limit.
Another way to view the color separation between stars and galaxies is within
the J-H vs. H-Ks color plane,
Figure 15. Here we include the stellar
main sequence track, showing the divergence of giants from dwarfs at
H-Ks > 0.3 mag. In addition, we show the K-correction track for
spiral galaxies derived from the models of Bruzual & Charlot (1993,
ApJ, 405, 538). When
the surface density of stars is high the extinction is also on the rise,
clearly seen in the right panel of
Figure 15.
At fainter flux levels, Ks > 13.5 mag, the scatter in the integrated
flux (and thus colors) is large enough that non-galaxies (i.e., double and
triple stars) can scatter above the J-Ks color limit and galaxies
can have colors that scatter below the limit to a degree that contamination
and completeness is significantly compromised if the J-Ks attribute
were used as the lone discriminant. Moreover, for all flux levels, a
J-Ks threshold would impart an undesirable selection bias against
blue galaxies. To minimize color biases, the J-Ks attribute can be
combined with the radial shape attributes to form a new powerful discriminant.
First, the color-color plots suggest a more optimum method to use
JHKs colors to measure the "redness" of a galaxy. Galaxies are not
only preferentially redder than 0.9 mag in J-Ks, but they also have
H-Ks values, >0.2 mag, redder than most stars. Hence, we define a
"color score" as the color distance in J-H vs. H-Ks space
from the line corresponding to J-Ks = 0.9 mag to within a scaling
factor. For objects redder than 0.3 mag in H-Ks, we also factor in the
H-Ks color to exploit this feature in the JHKs color
space. Mathematically, we express the "color score" as:
which adds the color "distance" (to within a scaling factor) from the dotted
line in Figure 15. For sources with
(H-Ks)>0.3 mag, the color score reduces to:
Figure 16 demonstrates the
combination of color score and WSH. This combination alone is
capable of providing
better than 95% reliability (Ks < 13.5 mag) with only a few percent
loss of galaxies to the total population. We can do better still by using all
of the attributes simultaneously with a decision tree classifier. It should be
emphasized that no sources are eliminated from the extended source
catalog by their color alone, but the color score is a necessary component
toward generation of a reliable galaxy catalog.
The Color Attribute
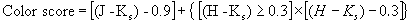

(Eq. IV.5.5)
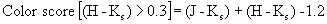

(Eq. IV.5.6)

|
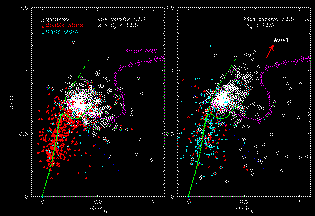
|
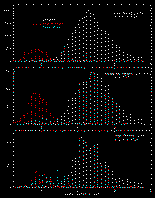 |
| Figure 14 | Figure 15 | Figure 16 |
Three classes of attributes have been discussed thus far: radial extent or
shape (SH, R1, R23), symmetry or azimuthal shape
(WSH, MSH, flux ratios) and flux or photo-metrics
(VINT, "color score", total flux, and central
surface brightness relative to the total flux). To determine the best
combination of parameters to use for galaxy discrimination we have a
nine-dimensional space to probe. Complicating matters, with a principle
component analysis we find that several of the attributes are highly
correlated (e.g., WSH and MSH, not surprisingly) and others
weakly correlated
(e.g., WSH and the bi-symmetric flux ratio),
which means that a simple or weighted combination of the attributes to form a
"super" attribute is not optimal. We may either combine a few of the attributes
that are not strongly correlated (e.g., color score and WSH and
R23), e.g., Figure 16,
or employ a decision tree induction method (Breiman et al. 1984, Classification
and Regression Trees) to more
effectively combine all or at least most of the attributes (with judicious
pruning; see below).
In the last few years, decision trees and their close cousins,
machine-learning artificial neural networks, have been used by astronomers to
aid image classification (e.g., Weir et al, 1995, AJ, 109, 2401; Odewahn et al.
1992, AJ, 103, 318; Salzberg et al. 1995, PASP, 107, 279; White 1997, in
Statistical Challenges in Modern Astronomy II, p. 135).
With fast computer technology these methods
provide an efficient means to analyze multi-dimensional data. We have adopted
one particular type of decision tree, called the oblique-axis decision tree,
but there are many others that would probably also be effective.
Decision tree methods, like "supervised neural networks," require a
training set of pre-classified data composed of all combinations of stars
(isolated, double, triple, etc.), galaxies, and artifacts. This "truth" set is
used to generate the decision tree, or a structured set of classification
rules. The tree divides the training set information into disjoint subsets,
each of which is described by a simple rule on one or more parameters. Using
the analogy of a tree, the rule structure contains "nodes" of branching test
points with the final nodes in the tree representing the "leaves" or final
classification. For example, one node might represent a test of the
WSH score, comparing the score to some threshold, T,
WSH score > T ?
NO: classify as non-galaxy
YES: continue to next node
This is an example of an "axis-parallel" decision. That is to say, the
parameter or object attribute embodies a set of hyperplanes (in the
multi-dimension phase space) that are parallel to each other.
Figure 17
demonstrates a two-featured, hyperplane: WSH
score vs. J mag with galaxies denoted by filled circles and
non-galaxies by
crosses. The non-galaxies are mostly double stars in this example. The dashed
parallel lines represent the axis-parallel "rules." To the right (or above)
the lines are the galaxies; to the left (and/or below) the lines are the
non-galaxies. Axis-parallel rules have the advantage of being simple to apply
and track within a large complicated tree. But it is obvious from the example
plot that a better rule is to use an "oblique" line separating the two
populations or features. The solid line in
Figure 17 is an example of an
oblique-axis ruling. An oblique decision tree uses both axis-parallel and
oblique-axis tests at the nodes. Mathematically, the node test has the linear
form:
where object O possesses n attributes, with a coefficients or
weights defining the n-dimensional hyperplane. For the reduced axis-parallel
case, the sum reduces to aj Oj > T.
Although oblique
hyperplanes are just a series of linear combinations, the total possible number
of solutions is very large and thus finding the correct one is daunting, if
not impossible under some conditions. In fact, the problem is NP-Complete, or
ultimately limited by the runtime of the machine. Fortunately, in practice
reasonable decision trees can be generated with clever deduction algorithms
and techniques to avoid "traps" or local minimum solutions.
Oblique Decision Tree Classifier
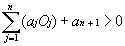

(Eq. IV.5.7)
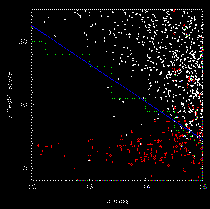 |
| Figure 17 |
One such package was developed by Murthy et al (1994, "A System for Induction of Oblique Decision Trees", JAIR, 2, 1) called OC1, or Oblique Classifier 1. OC1 uses random perturbations to walk around traps and arrive at satisfactory hyperplane solutions for each node. The resultant tree may require "pruning" or stripping of branches that add little to the final classification, or worse, detract from the correct solution due to over-fitting of the training set. OC1 applies pruning methods, e.g., Cost Complexity pruning (Breiman et al 1984, Classification and Regression Trees), which effectively prunes the decision tree by removing the insignificant or "weak" branches. For the problem of over-fitting, in addition to pruning, the best solution is to minimize the total number of attributes per node. For 2MASS galaxies, nine attributes including the integrated flux characterize each source. The attributes are correlated to one degree or another, so it is not obvious which can be eliminated from the decision tree process. A principal component analysis does indicate which parameters are key to the success of the decision tree. Additional trial and error experimentation with the training sets provide further clues as to the level of pruning that our decision tree requires. One disadvantage that decision trees have with classification of galaxies is that the final classification does not have an associated uncertainty or probability that the classification is correct. For 2MASS galaxies, we can "assign" a pseudo-probability by using a weighted average of the decision tree classifications for each band (which are computed independent of each other, except for the color attribute which; see below). These parameters are identified in the 2MASS database as "g_score" and "e_score" (see also Table 1).
The 2MASS star-galaxy separation problem is well suited to an oblique decision tree technique. Accordingly, we have applied the OC1 technique to large data (training) sets of 2MASS extended sources and non-galaxies (stars, double stars, triples, etc.). The training sets were constructed by carefully analyzing large swaths of sky, including ones with galaxy clusters, low stellar density (high galactic latitude) and high stellar density (Galactic plane) fields, totally over 50,000 sources in over 1000 deg2 of sky. The training sets are comprised of galaxies, stars, double and triple stars, nebulae, artifacts and sources that cannot be decoded. Each source was visually examined with 2MASS image data and with independently-acquired optical-wavelength data, including deep high-resolution CCD images (typically at R-band) or images from the Digitized Sky Survey (DSS). The DSS is well matched to 2MASS, both having similar resolution and sensitivity (for normal color galaxies), at least outside of heavily-extincted regions. We also cross-identified with astronomical databases (e.g., NED and SIMBAD), and, for some cases in which the reddening is severe (for |b| < 5 to 10°, the DSS is largely ineffective), obtained additional radio or deep infrared data. Previously identified/catalogued sources in the Galactic plane tend to be foreground nebulae, such as H II regions, which have very red colors, J-Ks > 1.5 mag, typically redder than extragalactic sources. We assign categories as follows: (1) extended, (2) stellar or point-like, (3) double star, (4) triple star, (5) artifact, and (6) unknown. The latter refers to our inability to decipher the nature of some sources (almost exclusively low SNR objects). Artifacts arise from two primary sources: bright stars and transient events (e.g., meteor streaks). As a final caveat, there will always be cases in which the classification is incorrect (e.g., mistaking a faint double star for a galaxy), but our training sets are constantly scrutinized and cleaned of falsely-classified sources. We believe the training sets are reliable to better than 98% for sources as faint as SNR = 7.
The training sets are divided into three density domains: low stellar density fields (<103.1 stars deg-2 brighter than Ks=14 mag), moderate (103.1 to 103.6 stars deg-2), and high (>103.6 stars deg-2 brighter than Ks=14 mag). These are further divided into subsets depending on the integrated flux of the source. The latter step minimizes the severe dynamic range (in flux) that 2MASS must consider, from the brightest galaxies (Ks < 9 mag) to the faintest galaxies (Ks ~ 14 mag). The training sets are large and diverse and thus provide a suitable induction test bed for the decision tree algorithm. We find that the OC1 decision tree classifier improves the galaxy catalog reliability by several percent, from 91% to ~97% (for sources brighter than 13.5 mag at Ks), compared to just using simple CART or axis-parallel tests. The trend persists in regions of high stellar number density where double and triple stars are a serious contaminant. Future work to refine the decision trees will focus upon further pruning of the trees and upon possible elimination of "weak" and highly correlated attributes. It may also prove fruitful to evaluate other decision tree methods (for example those developed by Weir et al. 1995, AJ, 109, 2401; Fayyad 1994, in Artifical Intelligence AAAI-94, 6601) and, possibly, neural network methods, particularly if morphological classification is attempted with 2MASS imaging data.
viii. Bright Extended (Fuzzy) Stars
Bright fuzzy stars are identified using a separate algorithm within the
GALWORKS pipeline (Figures 1 and
2). This operation is
referred to as the "bright extended source" processor. The basic method is to
look for emission in and around the source at levels elevated above that
expected for a bright star characterized by the PSF. The following gives a
brief (high-level) description of the method. To date, no results from this
method have been publicly released.
This is a difficult task given that bright stars are rife with nearly
insurmountable complexities (see
below). The algorithm measures residual
emission around the bright star after nearby stars have been masked and the
source itself has been removed based on the shape of the PSF and the measured
flux of the star. We calculate the root mean square of the residual emission
vs. the mean background AND vs. a zero background (i.e., assume the true
background level is zero). The RMS values are then normalized by the measured
noise for the Atlas image as a whole. Stars with associated emission,
like reflection nebulae, will usually stand out in either measurement. Sources
with a significant RMS deviation from the norm are extracted to the 2MASS
database. A special catalog is to be released at some date in the future.
There are no set requirements for these kinds of objects and the completeness
and reliability of this supplemental catalog are unknown at this time. Examples
of sources found with this technique are shown in
Figure 18, from scans
crossing the Orion Trapezium and the Large Magellanic Clouds. The top row
shows J-band "postage stamp" images, middle row the H-band and bottom row the
Ks-band images. Each image is 50´´ in
width. The integrated flux for the example sources range from magnitude
5 to 7 at 2.2µm.
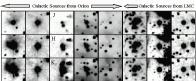 |
| Figure 18 |
There are some galaxies whose central surface brightness is too low to
be detected by the standard 2MASS procedure, but whose total integrated flux
is significant (at least with respect to the 2MASS Level 1 specifications).
These may include low surface brightness (LSB) galaxies, and dwarf or
intrinsically small galaxies. We will refer to these sources with the generic
moniker: low central surface brightness galaxies (LCSB). LCSB galaxies present
a different challenge to GALWORKS than the typical "normal" galaxy 2MASS
encounters. They are generally very faint (as measured in a standard aperture
for "normal" galaxies) and they do not have well defined cores;
see Figure 19
for examples of typical low central surface brightness galaxies found within
2MASS (Each image is 25´´ in width.) The
integrated flux of the example sources range from J=15 to 15.6 and
Ks=13.8 to 15.1 mag. The LSB galaxy nature of many of these sources
is confirmed with deep optical images. There are some examples of galaxies
observed to be low surface brightness in the near-infrared but normal in the
optical-typically blue spiral galaxies.
Low Central Surface Brightness Galaxies
 |
| Figure 19 |
The galaxy core is an important component for star-galaxy separation since many of the parametric measurements for star-galaxy separation are anchored to the core of the galaxy. The low central surface brightness detector (referred to as the LCSB processor) of GALWORKS is executed last in the chain of operations that comprise GALWORKS (see flowchart, Figure 2). The input to the LCSB processor is a fully cleaned Atlas image in each band, where stars brighter than some limit, typically Ks = 14.5 mag, and previously found extended sources have been entirely masked. The image is then blocked up (using three independent kernel sizes: 2×2, 4×4 and 8×8 pixels) and "boxcar" smoothed to increase the signal-to-noise ratio for large (but faint) objects normally hidden in the 1´´ correlated pixel noise. A block average is not the optimum method (as compared to a gaussian convolution, for example) but with pipeline runtime constraints it is a more satisfactory option.
The detection step consists of 3- threshold
isolation of local peaks in the blocked-up cleaned images. Source detections
are then parameterized (using the blocked and smoothed image) with the primary
measurements being: signal-to-noise ratio of the peak pixel, radial extent
(SH score), integrated signal-to-noise ratio, surface
brightness, integrated flux, and SNR measurements using a J+H+Ks
combined "super" image. The "super" image, in principle, provides the best
median from which to find faint LSB galaxies given the effective increase in
the signal-to-noise ratio. In practice, the "super" image only increases the
SNR by approximately 30%-50% for normal (i.e., J-Ks ~ 1 mag) galaxy
colors. Faint stars remaining in the cleaned image have a relatively low SNR
since most of their light is confined to a few pixels that are averaged with
blank sky in the blocking and boxcar-smoothing step. Galaxies, on the other
hand, will add up since their light is distributed over a larger area.
threshold
isolation of local peaks in the blocked-up cleaned images. Source detections
are then parameterized (using the blocked and smoothed image) with the primary
measurements being: signal-to-noise ratio of the peak pixel, radial extent
(SH score), integrated signal-to-noise ratio, surface
brightness, integrated flux, and SNR measurements using a J+H+Ks
combined "super" image. The "super" image, in principle, provides the best
median from which to find faint LSB galaxies given the effective increase in
the signal-to-noise ratio. In practice, the "super" image only increases the
SNR by approximately 30%-50% for normal (i.e., J-Ks ~ 1 mag) galaxy
colors. Faint stars remaining in the cleaned image have a relatively low SNR
since most of their light is confined to a few pixels that are averaged with
blank sky in the blocking and boxcar-smoothing step. Galaxies, on the other
hand, will add up since their light is distributed over a larger area.
The preliminary results for the LCSB processor demonstrate a reliability rate of about ~70 to 80% using a threshold on the "maximum" SNR (between 2×2, 4×4 and 8×8 blockings) of the "super" image. The major contaminants are faint stars and diffuse emission associated with bright stars. However, if a meteor streak (or other transient phenomenon) is present in the Atlas image(s), then numerous false sources are picked up as LSB galaxies.
We are still learning how to improve the reliability of sources coming from
the LCSB detector. It is important to note that these sources are nearly
always fainter than the Level 1 specifications (Ks > 13.5,
J > 15 mag) which means that there are currently no requirements on the
incompleteness and reliability. We do not anticipate significant completeness
failure for LSB galaxies brighter than Ks ~ 13.5 mag. The fainter LSBs,
however, will have to be detected and processed with the LCSB processor
described here and released in a future special catalog. Enhancements of the
algorithm described here are being studied, in particular, the multi-color
" 2 image" technique described in
Szalay et al. (1999, AJ, 117, 68) may prove to be a more robust and reliable
technique at finding LCSB galaxies in the 2MASS database. Further information
and some early science results with 2MASS LSB galaxies can be found in
Jarrett (1998, in The Impact of Near-Infrared Sky Surveys on Galactic and
Extragalactic Astronomy, p. 239) and Schneider et al. (1998, in The Impact of
Large Scale Near-IR Sky Surveys, p. 187).
2 image" technique described in
Szalay et al. (1999, AJ, 117, 68) may prove to be a more robust and reliable
technique at finding LCSB galaxies in the 2MASS database. Further information
and some early science results with 2MASS LSB galaxies can be found in
Jarrett (1998, in The Impact of Near-Infrared Sky Surveys on Galactic and
Extragalactic Astronomy, p. 239) and Schneider et al. (1998, in The Impact of
Large Scale Near-IR Sky Surveys, p. 187).
ix.Source Extraction
Sources that pass the star-galaxy discrimination tests and have an integrated
flux brighter than the mag limits: J= 15.5, H = 14.8, Ks = 14.3 mag
(MINUS the confusion noise for high source density fields), are extracted to
the 2MASS extended source database. In addition to the parameters described in
previous subsections, the source information includes various flags indicating
stellar contamination, cross-identification (with previously catalogued
large galaxies derived from the NASA Extragalactic Database) and
processing status. A list of the "standard" extended source parameters can be
found in the
Extended Source Catalog Record Format table.
For each extended source, a small "postage stamp" image is clipped from the
larger background-subtracted Atlas image. The stamp images are stored in J, H
and Ks fits-format data cube files (see Appendix D for an example
of a header). The image size is constrained by the final Kron or isophotal
radius, with a minimum diameter of 21´´ and a
maximum diameter of 101´´. The dynamic image
size reflects the practical limitation of the finite storage capability of the
2MASS database. The stamp image headers provide all of the information needed
to extract photometry, positions, etc., except the larger-area environment
that was used to remove a local background (above)
and evaluate contamination. For that reason the images include the background
removed during the process described above.
Since the background is already
removed, it is a simple matter at computing source fluxes, they can be directly
read (or summed within some aperture) from the images. The conversion of a
2MASS unit of flux ("dn" for data number, corresponding to the pixel value) is
as follows:
where f is the background-subtracted flux (in "dn" units),
m0 is the zero point calibration magnitude, and m is
the desired (calibrated) magnitude. Consider the example given in
Appendix B. Here the zero point
calibration at Ks is 20.111 mag, while the image "noise" (RMS of
the background) is 0.879 DN. It then follows that the
1-
The 2MASS extended source database is predominantly
composed of galaxies, with a much smaller population of double and triple
stars, at the 5 to 20% level depending on the stellar number density.
Large-angular size Galactic objects, such as HII regions, stars with
nebulosity, planetary nebulae, reflection nebulae, etc., are relatively rare
and generally confined to the Galactic plane and a few other star formation
sites around the Milky Way.
The extended source catalog is contaminated by a small 1-5% number of
artifacts.
These false sources are generated in the vicinity of bright stars, by
transient phenomenon, such as meteor streaks, and by infrared "airglow". Most
artifacts associated with bright stars are easily identified within the 2MASS
database using simple geometric removal algorithms, but which are not 100%
effective. Meteor streaks are more difficult to identify using automated
techniques, but in general their frequency is low. Airglow not only generates
false detections (especially under severe conditions), but it also
significantly affects the photometry of real sources. Examples of 2MASS
galaxies and various kinds of artifacts are given below.
i. Galaxies
The 2MASS extended source database contains galaxies ranging in brightness
from Ks=9 to 14 mag. This flux range is
constrained by the sensitivity of the survey and size limitations fixed by the
scale of the Atlas Image and the background removal process. Galaxies as large
as 3 or 4´ in diameter may be processed (if they are located near the
center of the Atlas image) but only the inner 2´ or so is examined in
detail (c.f. Figure 9). For very
large galaxies (>5´ in size), such as most of
the Messier objects, the only processing is to extract pieces of Atlas images
associated with the galaxy. At the faint end of the flux spectrum, it is
difficult to determine the size of the galaxy due to the resolution of the
survey, the elongation or asymmetry in the PSF, and the precise dither pattern.
For the most part, we can reliably measure isophotal sizes down to a radius of
7´´.
In Figures
20,
21, and
22,
a representative sample of galaxies from low stellar number
density fields is shown with their Ks-band postage stamp images.
The data come from scans passing through the Abell 3558, Hercules, & Abell
2065 clusters, as well as random non-cluster fields. A wide range in
morphology, surface brightness and integrated flux comprise the sample.
Figure 20
shows the brightest galaxies, ranging in total Ks-band flux from
9 to 13 mag. Each image is 60´´ × 60´´,
demonstrating several morphological classes:
elliptical (E), lenticular (S0, SA0), generic spiral (S), and complex
irregular, including double nucleus, interacting and pre-merger systems. The
next set of galaxies, Figure 21, represent
the faint limit at which the extended source catalog is both reliable
(>98%) and complete (>90%), with
Ks ranging from 13 to 13.5 mag. The size of each
image is 30´´ × 30´´. The final set of galaxies
(Figure 22)
represent the faintest galaxies resolved with 2MASS, with Ks
ranging from 13.5 to 15 mag, corresponding to a SNR range between
4 and 8. Each image is 20´´ × 20´´ in width. The
lowest surface brightness galaxies belong to this set, which are generally
detected only in J-band due to the blue color of most LSB-type galaxies. For
example, the last four galaxies in the set are detected in the J-band only.
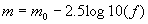

(Eq. IV.5.8)
 RMS in the Ks background is
20.250 mag/arcsec2 (note that this RMS noise is applicable to size
scales of ~2´´ × 2´´, corresponding to the effective
resolution of the 2MASS survey).
RMS in the Ks background is
20.250 mag/arcsec2 (note that this RMS noise is applicable to size
scales of ~2´´ × 2´´, corresponding to the effective
resolution of the 2MASS survey).
d. 2MASS Extended Source Objects
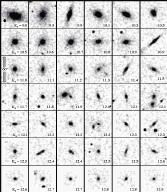
|
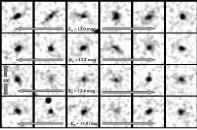
|
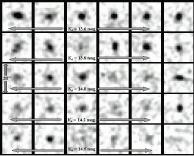 |
| Figure 20 | Figure 21 | Figure 22 |
When the source density is high, the confusion noise approaches the level of the atmospheric thermal background noise (see Appendix B). The probability of triple or multiple stars is significant and the ability to distinguish galaxies from multiple groupings of stars is strained. Nevertheless, a reliability of >80% is possible for most of the Galactic plane. Figure 23 gives examples of galaxies found in the Galactic plane, and for comparison, false extended sources (e.g., triple stars) found in the same areas. For the upper panels, the approximate Galactic coordinates are (240°, +4.5°), corresponding to a density of 4500 stars deg-2 brighter than 14 mag, and a differential confusion noise equivalent of 0.7 mag in a 10´´ aperture (see Appendix B). The integrated Ks-band fluxes range from 11.8 to 13.8 mag. The estimated visual extinction is ~1 mag and the J-Ks reddening is ~0.15 mag. Closer to the Galactic center (Figure 23, middle panels), coordinates (12°, +5.0°), the density of stars is over 30,000 deg-2, resulting in an equivalent differential K-band confusion noise of nearly 2 mags; yet, galaxies are still detected by 2MASS. The estimated visual extinction is now >2 mag and the J-Ks reddening is ~0.4 mag. Note the significant stellar contamination to the local environment of the galaxies. The integrated Ks-band flux ranges from 11.0 to 12.8 mag, indicative of confusion noise limits on the faint end detection spectrum. False detections are dominated by multiple stars (mostly triples and quadruples), a representative set is shown in the lower panels, Figure 23.
 |
| Figure 23 |
ii. Galactic Extended Sources
Nebulosity associated with bright stars (e.g., H II regions, PNs, clusters) and with molecular clouds (reflection nebulae, YSOs) typically appear as very bright and large extended sources (Figure 24). Since these objects are primarily located deep in the Galactic plane, contamination by foreground stars is unavoidable.
 |
| Figure 24 |
iii. Bright Stars and Artifacts
Bright stars are a major nuisance to any image-based survey. Off-axis stray
light can land just about anywhere on the focal plane, while dense
concentrations of light (e.g., diffraction spikes) are distributed
geometrically with respect to the optical axis. Features referred to as
"glints" and "ghosts" are focused or semi-focused reflections of light that
appear as slightly asymmetric point sources or flattened (low surface
brightness) extended sources. Not only do bright 2MASS stars (Ks
< 9 mag) produce diffraction spikes, halos, glints and ghosts, but
the brightest stars (Ks < 5 mag) generate
horizontal stripes that span the entire cross-scan (east-west axis) of the
scan, or a total of 8.5´ in length. Worse, these
stars are saturated, so we do not know their true integrated flux, making it
difficult to anticipate the strength of their associated stripe, spike and
persistence features (see below). Finally, bright stars induce another feature
unique to infrared arrays: latent residual or persistence ghosts. The central
core of a bright star leaves a residual signal after the array has been read
out. The residual persists for several seconds (and for the brightest stars,
many tens of seconds). Thus, a bright star will leave a "trail" of persistence
ghosts as the telescope shifts in declination. All of these bright star
artifacts, many of which strongly resemble galaxies, must be removed to meet
the Level 1 requirements. The 2MASS pipeline and GALWORKS in
particular, remove most of these artifacts
(see below). During the catalog generation phase (i.e., after the pipeline
reductions) we remove (or attempt to remove) the remaining artifacts that
contaminate the database.
Halos, stripes and spikes have a well-determined geometry with respect to
their progenitor, assuming that the integrated flux of the source is known.
GALWORKS determines their extent by measuring
their surface brightness, using limits based on the estimated total flux of
the star and the expected confusion noise as traced by the stellar number
density. Bright stars that saturate (K < 5 mag) may not have
well determined stripe intensity, spike length or persistence coverage.
Diffraction spikes extend several arcminutes for very bright stars; see, for
example, Figure 25,
which shows a magnitude 4 star in a J-band
Atlas image. Note the three horizontal stripes extended and flaring across the
entire 8.5´ of the field, and the persistence
ghosts trailing to the south of the bright star. An even more dramatic example
of spikes, ghosts, halo and stripes is seen in
Figure 26, which shows two
adjacent J-band images with a Ks~ -1
mag star (
Most meteor streaks have the unfortunate property of high surface brightness
coupled with severe elongation-similar to large highly inclined spiral
galaxies. Figure 27
demonstrates transient streaks in two different J-band
Atlas images. Note the sharp boundaries for the bright streak and the episodic
flaring for the fainter streak. The latter is, in fact, associated with
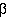 Pegasi) straddling the boundary. The
vertical spikes extend well beyond the image boundaries, while the halo
emission completely dominates both images. The persistence ghosts (trailing to
the south of
Pegasi) straddling the boundary. The
vertical spikes extend well beyond the image boundaries, while the halo
emission completely dominates both images. The persistence ghosts (trailing to
the south of 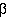 Peg) appear nearly as bright as
field stars. The influence of
Peg) appear nearly as bright as
field stars. The influence of 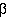 Peg extends
across scan boundaries as well, making it very difficult to identify and remove
artifacts during the pipeline reductions. Hence, the database is
significantly contaminated with false sources due to very bright stars such as
Peg extends
across scan boundaries as well, making it very difficult to identify and remove
artifacts during the pipeline reductions. Hence, the database is
significantly contaminated with false sources due to very bright stars such as
 Peg. Even in the post-processing stage, these
sources present a major clean-up challenge: internal telescope reflections
produce stripe/streak features extending over 1° in radius
from the center of
Peg. Even in the post-processing stage, these
sources present a major clean-up challenge: internal telescope reflections
produce stripe/streak features extending over 1° in radius
from the center of  Peg (see
Figure 27, right panel). In the vicinity
of the brightest stars (Ks < 0 mag) in the infrared sky, it may
not be possible to do an adequate artifact removal during the catalog
generation. Fortunately, there are only a handful of these problematic stars
spread throughout the sky.
Peg (see
Figure 27, right panel). In the vicinity
of the brightest stars (Ks < 0 mag) in the infrared sky, it may
not be possible to do an adequate artifact removal during the catalog
generation. Fortunately, there are only a handful of these problematic stars
spread throughout the sky.
 Peg
(Figure 26), discussed above. Meteor
streaks are
generally not identified in the pipeline reductions, resulting in false sources
populating the extended source database. Instead, false sources due to
"streaks" are removed during the catalog generation process: the one
identifying feature is that usually multiple detections (in some cases several
hundred sources) occur along the streak which can be identified with simple
database queries and cleaned from the catalogs accordingly.
Peg
(Figure 26), discussed above. Meteor
streaks are
generally not identified in the pipeline reductions, resulting in false sources
populating the extended source database. Instead, false sources due to
"streaks" are removed during the catalog generation process: the one
identifying feature is that usually multiple detections (in some cases several
hundred sources) occur along the streak which can be identified with simple
database queries and cleaned from the catalogs accordingly.
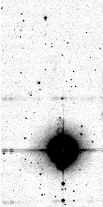
|
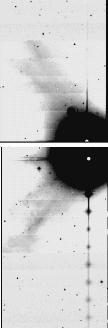
|
 |
| Figure 25 | Figure 26 | Figure 27 |
Yet more artifacts are produced by bright to moderately bright stars on the edges of scans, as well as additional artifacts from meteor streaks and background gradients (for example, airglow "bumps" that are not removed). Figure 28 illustrates some of the kinds of artifacts found in the extended source database. The first two (reading left to right) are the result of a "ghost" or "glint", most prominent in J band, to the southwest of the 8 to 9 mag progenitor star. The third column shows a false detection due to a flared diffraction spike from a star on the edge of an Atlas image. The fourth and fifth columns are examples of faint stars or faint galaxies located on or within the boundary of a horizontal stripe or meteor streak. The final column is a faint star boosted in flux by background airglow (note the prominent H-band emission). Many of these artifacts are successfully removed during the catalog generation process. The airglow artifact is probably the most insidious class of false detection since it is so difficult to discriminate from real galaxies or real interstellar nebulosity. The only way to minimize their effect is to avoid data with significant airglow. H-only extended-source detections should be treated with caution.
We project that at the end of the 2MASS survey we will have detected over 2 million extended sources as faint as ~2 mJy. At 2.2µm, 2MASS will discover galaxies never seen before in the "Zone of Avoidance" where the obscuring effects of Galactic dust and gas limit traditional surveys.
Much of the algorithmic development was driven by the practical need for computational speed and efficiency (e.g., background removal and LCSB detection). As processing power increases over time, it will be possible to implement more sophisticated methods, including more robust methods for detection of low surface brightness galaxies. Moreover, we continue to build and expand the classification "training sets" to improve the performance of the decision tree classifier, while other methods (e.g., supervised neural nets) may also prove to be powerful star-galaxy discriminents. Future improvements will be focused upon reliability (star-galaxy-artifact discrimination) and completeness for SNR sources (e.g., LCSB galaxies).
In the future we will discuss in detail the completeness and reliability that can be expected for the release catalogs. The scientific content is assessed with analysis of the source counts and redshift distribution, size and orientation distributions, JHKs colors, and coordinate position accuracy. Finally, we will discuss a method by which 2MASS extended sources may be used to identify and characterized galaxy clusters out to z ~ 0.2.
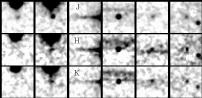 |
| Figure 28 |
The fundamental limits to 2MASS galaxy photometry are set by the accuracy
to which the background level can be determined, by the total signal-to-noise
ratio in the aperture used to report the flux of a galaxy, and by the zero-point
calibration used to adjust raw magnitudes onto a standard scale. Most of the
time, the dominant error is the Poisson noise due to the background summed
over the pixels used to make the photometric measurement and the uncertainty
in the standard background removal itself (see
above). However, a
significant portion of the 2MASS data is affected by high-frequency background
variation, which causes the photometric error to be larger for a small
fraction of the galaxies. There are two sources for such background variations,
one being atmospheric "airglow" and the other camera hardware related. In the
near-infrared, the background levels generally fluctuate due to airglow
emission, sometimes at very high spatial frequencies, particularly at 1.6
µm. In addition to airglow, 2MASS images include
electronic ("pickup") noise that is correlated and can, at times, be
comparable to the airglow component. Electronic pickup refers to image
features that are not of astronomical origin, but instead are associated with
the camera electronics. These features may manifest as periodic horizontal
stripes or abrupt jumps in the background level. The impact is mostly felt in
the galaxy photometry, where a systematic bias is introduced. This bias can be
as large as 20% in some cases, but is more typically 3 to 7% (usually an
overestimate of the galaxy flux). Examples of both forms of background
enhancement are given in Figure 29.
i. Summary of Standard Photometric Error
For the usual case where the galaxy flux is negligible compared to the
background flux, the measurement error in summing up the flux over n
pixels in the Atlas image is
where
GALWORKS also models and subtracts variations
in the background using a polynomial fitting scheme described
above. If
the background variations are small on time scales of a few seconds, the
fitting procedure is limited primarily by the effective RMS in the background
sky noise,
It is clear that the first term dominates the total error except when the
number of pixels within the aperture is very large, n >
104 (corresponding to a circular radius > 40 to 50 pixels).
This also assumes
that background variation is well behaved. Most galaxies detected in 2MASS are
small and faint, so the Poisson noise component (Eq. IV.5.9) should dominate
the total photometric error. Consider for example a Ks=13 mag
galaxy. The integrated flux is ~630 DN (or ~4.5 mJy) using a
typical Ks zero point magnitude of 20.0 mag (relating the calibrated
mag to the raw or "data number" flux; see Eq. IV.5.8). The typical size for a
galaxy of this brightness is about 16´´ in
diameter, corresponding to a circular aperture with ~200 pixels. The typical
Ks background pixel noise is ~1 DN (or 20 mag per
arcsec2). Using Eq. IV.5.10 and the integrated flux of the source,
we compute a SNR of 12.6 to 12.8, where the Poisson component is 25 to 70 times
larger than the background-fit uncertainty (i.e., the noise contribution from
the background fitting procedure is very small, only 1 to 4% of the
total photometric noise). For larger (and hence less common) galaxies,
the size of the galaxy must be greater then ~35´´
in diameter for the uncertainty in the background fit to become appreciable
(>10% of the total).
If the background variation requires a higher-power polynomial than a cubic,
then the error in the background will no longer be determined by the pixel
noise. Instead, the background error will result from the residual error after
a cubic polynomial is fit. This will be the case for severe airglow variation,
which can modulate on high spatial frequency scales (see left panel,
Figure 29), and from correlated
"electronic" noise (see right panel, Figure
29). Both
conditions can easily boost the total photometric noise by >50%.
Unfortunately, the 2MASS data reduction pipeline is not adequately designed to
quantify these severe background variations; and indeed, high-frequency
background variations may go undetected from scan to scan. We are exploring
methods at which detection and correction of severe 'airglow features" may be
possible, particularly for the H-band data. Fortunately, the hardware-induce
background variations are diminishing with maturity of the 2MASS survey.
Appendix A. Galaxy Photometry Error Tree
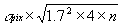

(Eq. IV.5.9)
 pix is the measured pixel
noise as measured using an entire Atlas image (512×1024 pixels).
The factor of 1.7 accounts for the smoothing introduced in the
Atlas image by the frame resampling and construction process, and the factor
of 4 results from the correlation of the flux in 1´´ pixels, due to
the 2´´ camera (raw frame).
pix is the measured pixel
noise as measured using an entire Atlas image (512×1024 pixels).
The factor of 1.7 accounts for the smoothing introduced in the
Atlas image by the frame resampling and construction process, and the factor
of 4 results from the correlation of the flux in 1´´ pixels, due to
the 2´´ camera (raw frame).
 pix. The fitting
procedure usually can match the background over regions as small as
~2´ to 3´. Empirical tests
indicate that the background fitting procedure is accurate to within 3 to 5%
of the RMS pixel noise (in the absence of abrupt background structure coming
from high-frequency airglow or electronic banding, which is usually the case
for the 2.2µm images). Since errors in the
background contribute systematically to all pixels in a galaxy smaller than
3´, this error contributes in proportion to the
number of pixels n. The total photometric noise variance is the quadratic sum
of these two terms
pix. The fitting
procedure usually can match the background over regions as small as
~2´ to 3´. Empirical tests
indicate that the background fitting procedure is accurate to within 3 to 5%
of the RMS pixel noise (in the absence of abrupt background structure coming
from high-frequency airglow or electronic banding, which is usually the case
for the 2.2µm images). Since errors in the
background contribute systematically to all pixels in a galaxy smaller than
3´, this error contributes in proportion to the
number of pixels n. The total photometric noise variance is the quadratic sum
of these two terms
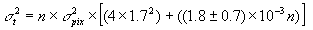

(Eq. IV.5.10)
 |
| Figure 29 |
ii. Adaptive Aperture Errors
Adaptive apertures (i.e., Kron and isophotal) come in two different shapes: circular and elliptical. Circular apertures are fully described by the radius, fit to the desired isophote. Elliptical apertures are described by three parameters, radius (semi-major axis), axis ratio and position angle, fit to the desired isophote. The fitting procedures introduce additional uncertainties. Here we assume the uncertainty due to the position of the isophote is negligible.
For the circular case, the radius has an error that is driven by background noise and contamination (i.e., stars near or within the isophote). Errors in the determination of that radius dominate the photometric error tree. Consider the typical case of a galaxy with an exponential profile. The integral flux over a circular aperture is
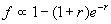 |
 |
(Eq. IV.5.11) |
where r is the aperture radius divided by the radial scale length of the galaxy profile. The flux error caused by the error in radius determination is
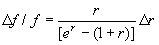 |
 |
(Eq. IV.5.12) |
For a disk scale length of 2´´, and typical
isophotal 20 mag arcsec-2 aperture radii of 6 to 8´´, the
flux error ranges between 0.08 and 0.19 ×
 r. The typical width or
uncertainty of the circular isophote is about 1´´, so
r. The typical width or
uncertainty of the circular isophote is about 1´´, so
 r=0.5 and the
resultant flux error ranges between 4-9%. The Poisson photon noise in an
aperture of this size gives typical flux errors of ~5-7%, and hence the radius
uncertainty is comparable to the photon-noise contribution for this
Ks~13 mag spiral galaxy case.
r=0.5 and the
resultant flux error ranges between 4-9%. The Poisson photon noise in an
aperture of this size gives typical flux errors of ~5-7%, and hence the radius
uncertainty is comparable to the photon-noise contribution for this
Ks~13 mag spiral galaxy case.
For elliptical aperture photometry, in addition to the radial uncertainty, two additional parameters (axial ratio and position angle) add to the total error budget. However, there is some positive compensation due to the fact that the orientation of galaxies is elliptically shaped; thus, optimal elliptical apertures minimize the background noise contribution and systematics due to measurement error in the background itself (above). Analysis of the 2MASS extended source database reveals that for 2MASS galaxies brighter than ~13 mag, the elliptical aperture photometry gives the most precise measurement of the galaxy flux. Note however that the elliptical aperture is vulnerable to contamination, especially in high source density regions, which makes it susceptible to large uncertainties if the ellipse parameters are inaccurate. For faint galaxies, the PSF shape and image resolution generally favor a circular aperture to that of an ellipse because the galaxies are so small that the ellipse parameters are highly uncertain.
As the surface density of stars exponentially increases near the disk of the
Galaxy, the probability of source contamination increases accordingly.
Likewise, near the Galactic plane, faint undetected stars significantly
increase the mean "noise" amplitude in the "background" sky. Both surface
density affects limit the source detection or completeness, and overall
reliability. Confusion arises from the appearance of an interloping star
within close proximity to the "beam" or point spread function pattern that
induces a significant flux bias (or "deflection") from the non-contaminated
flux due to the intended source (in our case, galaxy) near the beam center. A
convenient gauge for the severity of contamination or level of source
confusion, is the confusion "noise". In more practical form, the
confusion noise represents the change in surface brightness (i.e., sensitivity
limit) relative to the Galactic pole (where the confusion noise is
negligible), expressed in magnitude units. The confusion noise is directly
related to the stellar number density. In the 2MASS database the stellar
number density is referred to as the "density",
representing the base-10 log of the cumulative number of stars per
deg2 brighter than Ks=14 mag (see also
Table 1).
As the confusion noise becomes appreciable, it is one of the primary limits on
galaxy detection and reliability. Moreover, confusion decreases the accuracy
of both flux and position estimation. It is therefore important to understand
the confusion noise in terms of the ability to detect isolated sources and in
terms of identification of real extended sources, both of which require
threshold adjustment with confusion noise level.
i. Estimation of Confusion Noise
To estimate the additional component of "confusion" noise, we adopt the
methodology of Hacking (1987, PhDT) and Hacking & Houck (1987, ApJS, 63,
311). The idea is to
integrate the expected number of sources (with some flux distribution) within
the 2MASS effective beam,
where N is the integrated stellar number density (in deg2)
at flux f (in mJy). The aggregate variance due to background sources in
the beam, derived from
where Dc represents the outlier or "deflection" cutoff point
(in n-
Appropriate values for 2MASS Ks-band data are the following:
The confusion noise adds in quadrature to the already present background noise,
ii. Confusion Noise, Stellar Density and Galactic Coordinates
For relatively moderate flux ranges (e.g., V < 18; Ks < 14),
basic three-component models of the Galactic stellar distribution adequately
describe the number density of dwarf and giant stars comprising "disk" and
"spheroid" populations (Elias 1978, ApJ, 224, 453; Bahcall & Soneira 1980,
ApJS, 44, 73; Garwood & Jones 1987, PASP, 99, 453). Here we employ a
near-infrared modified variation on the Bahcall
& Soneira model, which predicts the stellar number density with ~90%
accuracy for most of the sky (|b| > 30°) and Ks < 14 mag,
and performs adequately (~80%) for the Galactic plane where patchy extinction
ultimately limits the utility of these simple models. The star-count model
predicts the stellar number density as a function of the Galactic coordinates,
which can then be used to calculate the approximate confusion noise.
A plot of the stellar number density as a function of the Galactic latitude
along two separate longitudes (50° and 130°) is shown in
Figure 30. The vertical dotted lines
represent the thresholds for what is deemed low stellar number density
(<103.1 stars deg-2), moderate density
(<103.6 stars deg-2), and high density
(>103.6 stars deg-2). The limit on high density is
partly driven by the relative density of triple stars vs. double or single
stars. As triple+ stars become appreciable, the ability to distinguish real
galaxies from close groupings of stars is greatly diminished. Finally, the
confusion noise (
Appendix B. Stellar Number Density and Confusion Noise
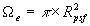 , where
, where
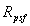 represents the effective
radius of the point spread function (typically ~2´´).
We may approximate the stellar flux distribution
with a power law of index
represents the effective
radius of the point spread function (typically ~2´´).
We may approximate the stellar flux distribution
with a power law of index  ,
,
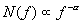

(Eq. IV.5.13)
 f,
d
f,
d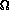 and
the differential stellar number density, is then
and
the differential stellar number density, is then
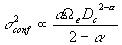

(Eq. IV.5.14)
 units; i.e., the detection threshold).
The source density index
units; i.e., the detection threshold).
The source density index  is approximately
equal to unity (more precisely ~0.85 for high latitude fields) as derived from
the log-log slope of the N vs. Ks cumulative star count
curve, ~0.35 for the NGP and slightly steeper at higher densities (Jarrett
1992, PhDT). Letting
is approximately
equal to unity (more precisely ~0.85 for high latitude fields) as derived from
the log-log slope of the N vs. Ks cumulative star count
curve, ~0.35 for the NGP and slightly steeper at higher densities (Jarrett
1992, PhDT). Letting 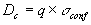 ,
we may express the confusion noise
as a function of the stellar number density, N(flim), at the
limiting flux, flim, and the deflection cutoff, q,
,
we may express the confusion noise
as a function of the stellar number density, N(flim), at the
limiting flux, flim, and the deflection cutoff, q,
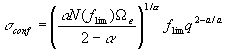

(Eq. IV.5.15)
 = 0.9,
= 0.9,
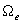 = 13.6 arcsec2 (4´´ beam),
flim = 1.8 mJy (corresponding to Ks=14 mag), and
q between 3 and 5; the confusion noise has units of mJy.
= 13.6 arcsec2 (4´´ beam),
flim = 1.8 mJy (corresponding to Ks=14 mag), and
q between 3 and 5; the confusion noise has units of mJy.
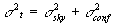 ,
raising the overall noise and
surface brightness of the background light. We desire to express the change in
the background surface brightness due to confusion noise as a function
of the stellar number density. We can turn the confusion noise into a surface
brightness by dividing by
,
raising the overall noise and
surface brightness of the background light. We desire to express the change in
the background surface brightness due to confusion noise as a function
of the stellar number density. We can turn the confusion noise into a surface
brightness by dividing by 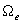 .
For the
background sky noise we adopt a value of 20.0 mag/pixel (typical for 2MASS 2.2
µm images). To convert the sky noise per pixel to
an equivalent surface brightness within the PSF beam, we need to divide by
.
For the
background sky noise we adopt a value of 20.0 mag/pixel (typical for 2MASS 2.2
µm images). To convert the sky noise per pixel to
an equivalent surface brightness within the PSF beam, we need to divide by
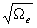 to account for the noise limit after
averaging over a 4´´ diameter. Accordingly, we
arrive at a sky noise surface brightness of 21.6 mag/arcsec2,
representing the value at the north Galactic pole (NGP), which is negligibly
affected by confusion from stars. The confusion noise (in
to account for the noise limit after
averaging over a 4´´ diameter. Accordingly, we
arrive at a sky noise surface brightness of 21.6 mag/arcsec2,
representing the value at the north Galactic pole (NGP), which is negligibly
affected by confusion from stars. The confusion noise (in
 mag units) is relative to the NGP sky surface
brightness noise (in a 4´´ diameter beam). The
Ks-band confusion noise as a function of the total integrated
stellar number density (flim < 1.8 mJy, or Ks
< 14 mag) is plotted in
Figure 30, described below, assuming a
beam size of 4´´,
mag units) is relative to the NGP sky surface
brightness noise (in a 4´´ diameter beam). The
Ks-band confusion noise as a function of the total integrated
stellar number density (flim < 1.8 mJy, or Ks
< 14 mag) is plotted in
Figure 30, described below, assuming a
beam size of 4´´,  = 0.9 and
q between 3 and 5.
= 0.9 and
q between 3 and 5.
 mag) appropriate to the
stellar number density is plotted in
Figure 30 (denoted with a cross-hatching, showing the detection threshold
range in q between 3 and 5), with the confusion noise
axis located at the right of the plot. Here the confusion noise (in mag units)
is relative to the equivalent sky background surface brightness
(1-
mag) appropriate to the
stellar number density is plotted in
Figure 30 (denoted with a cross-hatching, showing the detection threshold
range in q between 3 and 5), with the confusion noise
axis located at the right of the plot. Here the confusion noise (in mag units)
is relative to the equivalent sky background surface brightness
(1- detection limit) measured at high galactic
latitudes (i.e., NGP), equal to 0.0016 mJy (in a 4´´ circular
diameter beam) or 21.6 mag at 2.2 µm. This relative confusion noise is
called the "differential" confusion noise above.
detection limit) measured at high galactic
latitudes (i.e., NGP), equal to 0.0016 mJy (in a 4´´ circular
diameter beam) or 21.6 mag at 2.2 µm. This relative confusion noise is
called the "differential" confusion noise above.
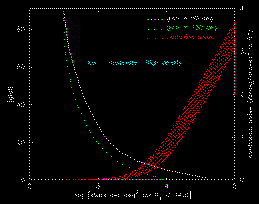 |
| Figure 30 |
The 2MASS Extended Source database contains over 400 parameters per source,
most of which are related to photometry. The public-accessible catalogs are
derived from this database. In Table 1
a condensed list is
given of the most important parameters in the catalogs. The list includes
positions, ellipse-shape geometry, photometry, surface brightness, star-galaxy
discrimination scores, symmetry, and "probability of extendedness" (see
above). The parameter name represents the actual
designation used in the catalogs and database.
For galaxy photometry and colors, we recommend the fiducial Ks-band
20 mag arcsec-2 ellipse-aperture measurements only for brighter
galaxies. However, for smaller galaxies (comprising most of the catalog) the
fixed R=7´´ circular-aperture values are the most
robust flux measures; see Table 1.
For each flux measure
there is an associated confusion flag, where a non-zero value indicates
stellar contamination.
For each extended source, a small "postage stamp" image is extracted from the
J, H and Ks Atlas images, with the background removed from each band
(see above). The image size is scaled by the final
Kron or isophotal diameter, with a minimum diameter of 21´´ and a
maximum diameter of 101´´. The multi-band
information is stored in a FITS cube, with the J image occupying the first
plane, H in the second plane and Ks in the third plane. The header
(see example below) contains the following information: catalog identification
(e.g., NED name, if any), observation date and time, equatorial coordinate
information, median background level before removal and the background
"noise", PSF "shape" value (representing the radial extent of the PSF at the
time of the observation; see above and
Eqs. IV.5.2 and IV.5.3), zero point
calibration magnitudes and the airmass. The background and "noise" values are
given in "dn" (or data number) units. See Eq.
IV.5.8 (above) for a conversion of "dn" flux units to
calibrated magnitudes.
bitpix = -32 [Last Updated: 2000 Feb 18; by T. Jarrett, T. Chester, S. Schneider,
S. Van Dyk, & R. Cutri]
Appendix C. Extended Source Catalog Parameters
Appendix D. 2MASS Extended Source Data Cube FITS Header
NAXIS = 3
NAXIS1 = 101
NAXIS2 = 101
NAXIS3 = 3
BSCALE = 1.
BZERO = 0.
GID = '000228 ' / 2MASS ID #
NNAME = 'NGC_4551' / NED Cat Name
ScanNo = '065 ' / Scan Number
CoaddNo = '256 ' / Coadd Number
ORDate = '980115n ' / Observation Ref Date (yymmdd)
UT_DATE = '980115 ' / UT Date of Frame (IC) (yymmdd)
UT = '11:04:07.23' / Time of Frame (IC) (sxgsml)
EQUINOX = 2000. / Equinox
CTYPE1 = 'RA---SIN' / Orthographic Projection
CTYPE2 = 'DEC---SIN' / Orthographic Projection
CRPIX1 = 51.
CRPIX2 = 51.
CRVAL1 = 188.9082336 / RA at Frame Center, J2000 (deg)
CRVAL2 = 12.26402664 / Dec at Frame Center, J2000 (deg)
CROTA2 = -0.009442620911 / Image Twist E of N, J2000 (deg)
CDELT1 = -0.0002777777845 / Axis 1 Pixel Size (degs)
CDELT2 = 0.0002777777845 / Axis 2 Pixel Size (degs)
RA = 188.9082336 / RA at Frame Center, J2000 (deg)
DEC = 12.26402664 / Dec at Frame Center, J2000 (deg)
JSKYVAL = 115.1816559 / GALWORKS J Sky Measurement
JSKYSIG = 0.5367393494 / GALWORKS J Noise Measurement
HSKYVAL = 492.6220398 / GALWORKS H Sky Measurement
HSKYSIG = 1.073829651 / GALWORKS H Noise Measurement
KSKYVAL = 277.62323 / GALWORKS K Sky Measurement
KSKYSIG = 0.8794555664 / GALWORKS K Noise Measurement
CALID = ' CALIBRATED' / Calibration ID
JSEESH = 0.9869999886 / Seeing J shape parameter
HSEESH = 0.9620000124 / Seeing H shape parameter
KSEESH = 0.9380000234 / Seeing K shape parameter
JMAGZP = 21.1258 / Calibrated J zero point from CALMAN
HMAGZP = 20.7288 / Calibrated H zero point from CALMAN
KMAGZP = 20.1106 / Calibrated K zero point from CALMAN
AMASS_FC= 1.118124962 / Airmass (aprox) at this position
ORIGIN = '2MASS ' / 2MASS Survey Camera
Previous page. Next page.
Return to Explanatory Supplement TOC Page.