INTRODUCTION
This document summarizes various development issues in connection with the PSFMAKE program, starting in October 2000. The first order of business was to diagnose and treat the anomalous trend in the chi squared values, characterized by anomalously low values for the brighter sources. The effect is most prominent at J-band, and is typified by 990918n/j061_fig1.
This behavior was found to be due to improper weighting of the residuals in the estimation of the PSF variance map. I had used the procedure that I outlined in the PSFMAKE explanatory document, in which I made an approximation based on a seeing-dominated noise model for the estimator stars. I've since found that it was not necessary to make such an approximation, and have derived an optimal solution to that problem (I'll update the explanatory document soon).
The results for that scan now look like:
with 990918n/j061_fig2.
UPDATES
Nov 2: Test the new PSFs using PROPHOT
The scan chosen was 990928n/s084, corresponding to a fairly high density region of the Galactic plane -- this scan was one of those used for an extensive set of tests about a year ago. The set of J-band PSFs for this scan were generated using the new version of PSFMAKE, and the PROPHOT results for this band are presented in the plot 990928n/j084_Nov2.
An unfortunate characteristic of that plot is the kink in the distribution of delta-mag versus magnitude.
Nov 8: Getting rid of the kink.
The kink in delta-mag v. mag was found to be due to an effect encountered
previously, namely Helmholtz ringing. This is manifest as a set of
diffraction-like rings surrounding the PSF, and is caused by the effects
of inadequate sampling on both the sinc interpolation and the linear
estimator used in PSF generation. The elegant way to remove it is by
using a finer grid. This, however, results in a large increase in
computation time. A cruder, but effective, alternative is to truncate
the PSF inside the 1st Helmholtz ring. After doing this, PSFMAKE gives
990918n/j061_fig3.
A new set of PSFs was generated on this basis, and PROPHOT rerun for
990928/j084. The results are shown in the plot
990928n/j084_nov8, in which the
delta-mag points represent (Fitted - Amag02).
Subject to further testing, it looks as if we have now achieved:
(1) Chi squared values distributed about unity.
(2) A flat (trendless) distribution of delta-mag.
(3) No systematic offset between the PSF-fitted and aperture magnitudes.
A complete set of production psfs has been generated for all hardware periods
in the northern and southern hemispheres. Variance maps were generated using
pixel gains estimated on the fly. These pixel gains were estimated from the
local sky background (in an annulus around each calibrator star), assuming
a constant value of read noise. The assumed values of read noise (in units
of electrons) were:
North:
J: 37.6
H: 42.2
K: 43.7
South: 46.0 at all three bands.
Plots of estimated gain as a function of time for all of the hardware periods
are as follows:
South
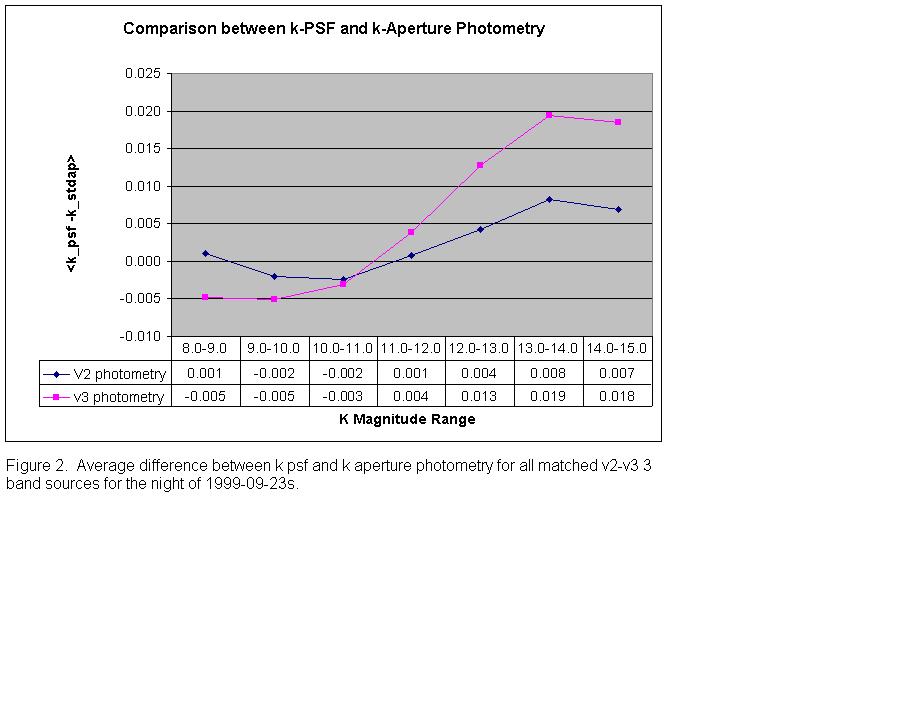
May 10, 2001: UPDATE ON MAGNITUDE-DEPENDENT FLUX BIAS.
Rae Stiening recently alerted us to the fact that a magnitude-dependent
flux bias is still present, as evidenced by his plot of delta-mag v. magnitude
for the Version 3 processing of 990923s:
The magnitude-dependent bias is an effect encountered previously (see, for
example, the Nov 8, 2000 update). It is due to the
interaction between a slightly distorted PSF and the
nonuniform weighting of the PSF in the parameter estimation process.
In the parameter estimation, different parts of the PSF are weighted
differently according to the magnitude of the source;
for the bright stars, which are seeing-error-dominated, relatively little
weighting is given to the central portion of the PSF, while for the faint
stars, the weighting is much more uniform.
The distortion of the PSF is due to Helmholtz ringing caused by undersampling
during the application of the linear estimator used in the PSF generation
process. The undersampling was a compromise arrived at from considerations
of cpu time. The resulting distortion of the PSF is primarily in the wings,
at around the few-percent level and below.
The distortion effects can not be expected to be better for the current
set of Version 3 PSFs than the original Version 2 ones, since both were
generated on the same undersampled grid.
The fact that the magnitude bias is somewhat worse now than it was
for Version 2 is because we are now weighting the PSF differently in order
to produce the proper chi square distribution.
Note, however, that the Version 3
PSFs are superior in other respects, such as signal to noise ratio and the
behavior of the reduced chi squared which now peaks around unity over the
entire magnitude range.
Possible solutions:
(1) Regenerate the PSFs on a finer grid.
(2) During PSF fitting, apply a weighting function which de-emphasizes the
PSF wings.
Possibility (2) has been implemented in the current version of prophot used
in rtb tests. An example of its performance is shown by the following 3
plots of the magnitude bias for 990928n, s084 at H band:
We are investigating the feasibility of implementing
possibility (1) in time for final reprocessing.
May 20, 2001: A PROCEDURE FOR OVERCOMING PSF DEFICIENCIES.
After further consideration of the problem described above, I believe the
following procedure will overcome the problems of Helmholtz-type ringing
in the PSF without the necessity of going to a finer grid with its associated
computational expense:
Step (1): Generate an initial PSF in the same manner as is done currently,
i.e. a linear estimator based on sinc interpolation, on a
less-than-critically-sampled grid.
Step (2): Obtain a correction to this initial PSF by first calculating the
residuals with respect to the data pixels, binning them into the same grid
as above using a boxcar window, and finally making a maximum likelihood
estimate of the correction from the set of residuals at each point on the grid.
What have we lost by doing this? The answer, of course, is that we've
lost some high-spatial-frequency information in the boxcar averaging step.
However, this averaging is applied to
the *correction* rather than to the initial PSF, and therefore comes in
only as a 2nd order effect. Therefore, although we haven't beaten the
sampling theorem by doing this, we have managed to alleviate the most
serious effects of undersampling inasmuch as they affect the photometric
properties of the PSF.
The following figure shows an example of the PSF correction (from 991024s,
scan 44, at J band), and represents essentially the distribution of data
residuals with respect to the initial (distorted) PSF.
The field of view is 5 focal-plane pixels; only positive
residuals are shown (dark), and are clipped at quarter-maximum to
bring out better the low level features. The full range of the residual
image is -5% to +4%, with respect to the PSF peak.
The Helmholtz rings are clearly
visible. It is the 2nd-order (middle) ring which is most responsible for
the magnitude-dependent flux bias.
May 21, 2001: PROPHOT RESULTS USING PSF CORRECTION
PSFs were generated using the above procedure, for 991024s/s044 at all 3 bands.
PROPHOT was then run on this scan using a single PSF per band. The
following plots show the resulting magnitude bias (fitted - aperture) as
a function of magnitude. Also shown, for comparison, are the corresponding
results for the recent RTB run on this scan (using the Version 3 PSFs, and
a "fix" in PROPHOT).
J magnitude bias: New result compared to RTB
Here are the corresponding comparisons with Version 2:
J magnitude bias: New result compared to Version 2
An additional problem encountered in the recent RTB runs has been the existence
of excessively high sigmas for the fitted magnitudes. The following set
of plots enables a comparison of the magnitude sigmas between the new results,
the RTB results, and the Version 2 results:
J magnitude sigmas: New
J magnitude sigmas: RTB
J magnitude sigmas: Version 2
I draw the following conclusions from the above results:
(1) The magnitude bias of the new (corrected) PSFs is noticeably reduced from
the Version 3 PSFs used in the RTBs (even with the "fix" in PROPHOT),
and is somewhat reduced from Version 2.
(2) The magnitude sigmas of the new (corrected) PSFs are quite healthy.
They are significantly less
for than the RTB results, and are even less than for Version 2. The latter
is a manifestation of the fact that the new PSFs do not have the anomalously
low chi squared values for bright sources that were a problem in Version 2.
I believe these results argue for regeneration of the PSFs.
March 19, 2001: Gain history
H magnitude bias: New result compared to RTB
K magnitude bias: New result compared to RTB
H magnitude bias: New result compared to Version 2
K magnitude bias: New result compared to Version 2
H magnitude sigmas: New
K magnitude sigmas: New
H magnitude sigmas: RTB
K magnitude sigmas: RTB
H magnitude sigmas: Version 2
K magnitude sigmas: Version 2