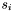 has four corners
has four corners 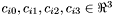 , with edges linking corners 0 and 1, 1 and 2, 2 and 3, and 3 and 0. Each great circle edge can be specified with a single vector perpendicular to the plane passing through the origin and both edge vertices :
, with edges linking corners 0 and 1, 1 and 2, 2 and 3, and 3 and 0. Each great circle edge can be specified with a single vector perpendicular to the plane passing through the origin and both edge vertices : | Contents | |
This page describes algorithms which determine how many such scans cover a particular position on the sky - a quantity which roughly indicates the expected number of apparitions of a single astronomical source located at that position, assuming an ideal instrument and observation conditions.
A scan 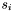 has four corners
has four corners 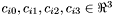 , with edges linking corners 0 and 1, 1 and 2, 2 and 3, and 3 and 0. Each great circle edge can be specified with a single vector perpendicular to the plane passing through the origin and both edge vertices :
, with edges linking corners 0 and 1, 1 and 2, 2 and 3, and 3 and 0. Each great circle edge can be specified with a single vector perpendicular to the plane passing through the origin and both edge vertices :
![\[ n_{i0} = \frac{c_{i0} \wedge c_{i1}}{\Vert c_{i0} \wedge c_{i1} \Vert},\; n_{i1} = \frac{c_{i1} \wedge c_{i2}}{\Vert c_{i1} \wedge c_{i2} \Vert}.\; n_{i2} = \frac{c_{i2} \wedge c_{i3}}{\Vert c_{i2} \wedge c_{i3} \Vert},\; n_{i3} = \frac{c_{i3} \wedge c_{i0}}{\Vert c_{i3} \wedge c_{i0} \Vert} \]](form_107.png)
The corners are numbered such that they appear in counter-clockwise order when viewed from outside the unit-sphere in a right handed coordinate system.
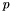 is defined as the number of scans covering
is defined as the number of scans covering 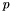 .
.
For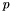 to lay inside a scan
to lay inside a scan 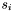 , it must satisfy the following four conditions :
, it must satisfy the following four conditions :
![\[ p \cdot n_{i0} \geq 0,\; p \cdot n_{i1} \geq 0,\; p \cdot n_{i2} \geq 0,\; p \cdot n_{i3} \geq 0 \]](form_109.png)
that is, 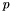 must lay inside each of the edge planes.
must lay inside each of the edge planes.
 is to perform the test above for each existing scan.
is to perform the test above for each existing scan. Since the databases being processed involve apparitions from up to 70000 scans, this would involve performing between 70000 and 280000 dot products and comparisons to determine the scan coverage of a single position.
Because scan coverage is likely to be computed for the position of every group generated by WAX, this algorithm is unacceptable.
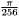 radians). Each band is further subdivided into equal width lanes, with a minimum lane width of 0.3 degrees. This subdivision scheme is essentially identical to the one used for apparitions (see Lane Subdivision), but is performed on scans and on a much coarser scale.
radians). Each band is further subdivided into equal width lanes, with a minimum lane width of 0.3 degrees. This subdivision scheme is essentially identical to the one used for apparitions (see Lane Subdivision), but is performed on scans and on a much coarser scale. If a list of overlapping scans were stored for each lane, this coarse subdivision scheme would already drastically reduce the number of coverage tests required for a position. However, there are datasets which contain clusters of more than 3000 scans, stacked virtually on top of eachother. Simple binning as described would still incur a cost of up to 12000 dot products per position for these cases.
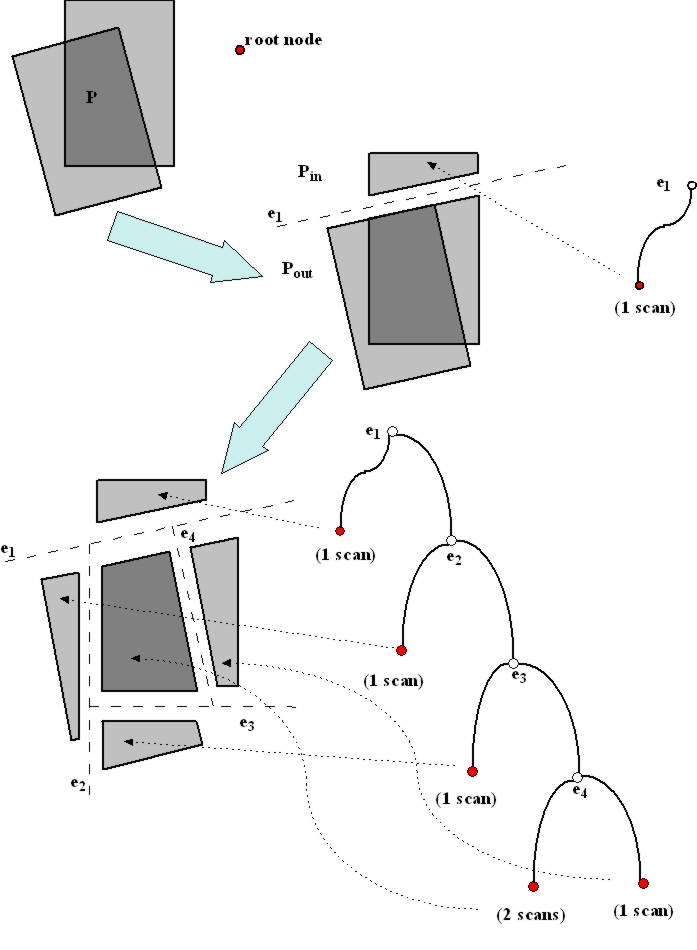
Therefore, instead of storing a list of overlapping scans for each lane, the overlapping scans are used to generate a Binary Space Partitioning (BSP) tree. This tree is stored for each lane in every band, and is used for all coverage computations.
Let 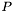 be the set of polygons corresponding to scans.
be the set of polygons corresponding to scans.
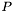 , take an as yet unconsidered edge plane and use it to split
, take an as yet unconsidered edge plane and use it to split 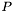 into two polygon sets, one containing polygons completely inside the chosen edge plane,
into two polygon sets, one containing polygons completely inside the chosen edge plane, 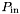 , the other containing polygons completely outside,
, the other containing polygons completely outside, 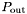 . Polygons straddling the edge plane are themselves split into an inside and outside polygon (using the aforementioned clipping algorithms).
. Polygons straddling the edge plane are themselves split into an inside and outside polygon (using the aforementioned clipping algorithms).  is non-empty and contains a polygon with an as yet unconsidered edge plane, feed
is non-empty and contains a polygon with an as yet unconsidered edge plane, feed  to step 1. Otherwise, store the number of polygons in
to step 1. Otherwise, store the number of polygons in  . Then continue with step 3.
. Then continue with step 3.  is non-empty and contains a polygon with an as yet unconsidered edge plane, feed
is non-empty and contains a polygon with an as yet unconsidered edge plane, feed 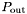 to step 1. Otherwise, store the number of polygons in
to step 1. Otherwise, store the number of polygons in  .
. The process, illustrated below, produces a binary tree in depth first order, where nodes correspond to splitting planes and leaves are convex polygons inside of which scan coverage is constant (no leaf contains a scan edge).
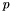 is equivalent to finding the BSP tree leaf containing
is equivalent to finding the BSP tree leaf containing 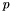 . This is easily done, starting with a current node equal to the root node of the tree :
. This is easily done, starting with a current node equal to the root node of the tree :
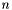 of the current node, determine whether
of the current node, determine whether 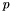 belongs to the inside or outside child of the current node :
belongs to the inside or outside child of the current node : 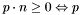 belongs to the inside child
belongs to the inside child 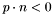 ),
), 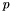 belongs to the outside child
belongs to the outside child 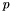 is a node, set the current node to equal the child and continue with step 1.
is a node, set the current node to equal the child and continue with step 1. 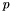 is a leaf. Since scan coverage is constant inside each leaf, the scan coverage for
is a leaf. Since scan coverage is constant inside each leaf, the scan coverage for 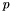 has been found and the computation is complete.
has been found and the computation is complete. This process is illustrated below, with empty leaves (those with 0 scan coverage) omitted from the diagram.
The ascent of the tree will involve a number of nodes no greater than the maximum tree depth. The worst cases encountered in practice (stacks of 1500 to 3500 scans) result in tree depths between 12 and 40. Since one dot product is performed for each node visited in the BSP tree, the algorithm performs at most 40 vector dot products for a scan coverage computation (as opposed to between 1500 and 14000).
The WAX software currently only supports small circular search regions, specified as a search region center, 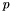 , and a search radius,
, and a search radius,  . A position
. A position 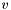 is inside the area if and only if
is inside the area if and only if 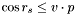 .
.
Finding the leaves intersecting the search area is accomplished as follows, starting with a current node equal to the root node of the tree :
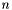 of the current node, determine whether the search area intersects the inside and outside children of the current node.
of the current node, determine whether the search area intersects the inside and outside children of the current node. 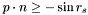 , then the search region touches the inside child :
, then the search region touches the inside child : 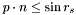 , then the search region touches the outside child :
, then the search region touches the outside child :
Picking a search radius 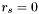 will produce a minimum and maximum scan coverage equal to the scan coverage for
will produce a minimum and maximum scan coverage equal to the scan coverage for 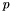 .
.
 1.3.8
1.3.8