Point Source Noise Estimation From PROPHOT Uncertanties

Introduction

Chas Beichman suggested that the distribution of uncertainties quoted for the point source photometry from PROPHOT can be used to estimate the effective point source noise in a 2MASS survey scan. This noise level can then be used to define the signal-to-noise threshold for detections to be included in the incremental release catalog. The advantage of such an estimator is that is intimately tied to the photometry algorithms, and it can be calculated easily from source listings in the database, so will not require time-consuming restoration of processed data from tape.

This suggestion is based on the assumption that the measurement uncertainty returned by the PROPHOT profile-fitting routines accurately samples the true photometric noise distribution. The PROPHOT uncertainty incorporates the photon noise in the local background (sky) and the photon noise in the source, as well as the accuracy to which the profile of the source matches the template of a true points source. A number of effects will increase the uncertainty measured for individual objects such as source crowding, background variations, both astrophysical and atmospheric, seeing fluctuations, etc. These effects should produce a tail to higher flux levels in the error distribution, but there should be an identifiable mode that characterizes the true point source noise distribution in the scan.

PROPHOT Flux Error Distrbutions

Figures 1 through 3 below show plots of the flux uncertainty reported by the profile-fitting photometry as a function of source flux density for non-artifact R2-R1 sources in three sample 2MASS scans that span a broad range of source density. For the analysis described in this report, magnitude-to-flux conversions were made using flux-for-zero magnitudes values of 1.603e6, 1.075e6, and 6.981e5 mJy, for J, H and K_s, respectively. Scan 008 from the night of 980609n covers a relatively low density field with a total of 5,905 detections. Scan 022 from the night of 980627s has 11,314 detections, and scan 051, also from the night of 980627s, covers a very high density region with 94,694 detections.

Figure 1 - Flux measurement uncertainties plotted versus flux density (both in mJy) for scan 008 on 980609n.

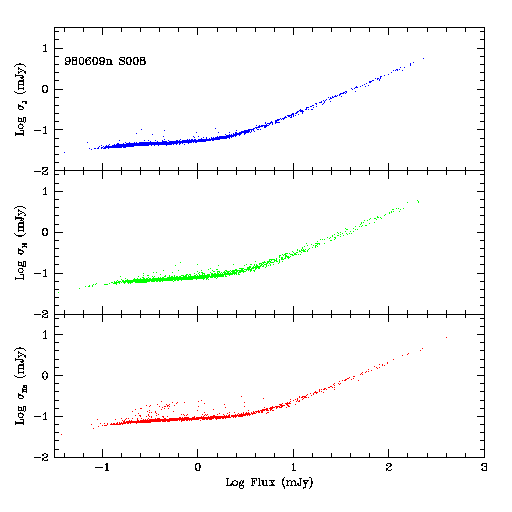
Figure 2 - Flux measurement uncertainties plotted versus flux density (both in mJy) for scan 022 on 980627s.

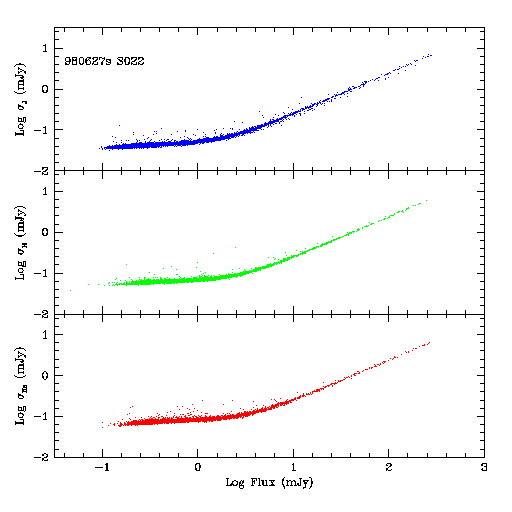
Figure 3 - Flux measurement uncertainties plotted versus flux density (both in mJy) for scan 051 on 980627s.

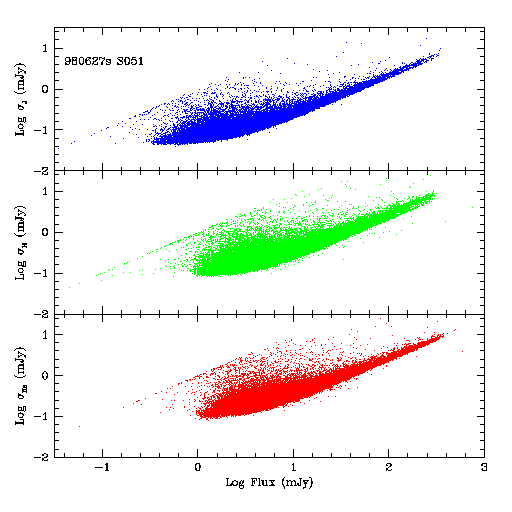
At low source flux densities, where the uncertainties are dominated by background photon noise, the uncertainties remain relatively constant, increasing only slowly with source brightness. Because most sources detected in a scan have low flux density, this suggests that the PROPHOT uncertainty is a reasonable way to measure the characteristic noise of a scan. For brighter objects, the uncertainties approach the familiar constant SNR regime where source photon noise and pixelization errors become important. The noise distribution in the very high density field shows a number of "features" caused by un-flagged artifacts.

Measuring the Characteristic Point Source Noise in a Scan

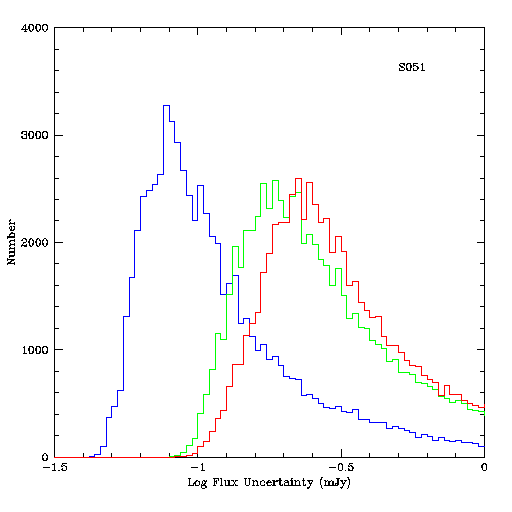
Figures 4-6 show histograms of the PROPHOT measurement errors for the three scans. All three histograms show clear peaks in the noise distribution for faint objects, and these peaks can be used as simple mode estimators for the error distributions. The roll-offs toward fainter flux levels are approximately Gaussian for the low and moderate density scans, and more complex for the high density scan. The tails toward higher noise levels due to crowding and other non-Gaussian effects are apparent.

Figure 4 - Histogram of PROPHOT flux uncertainties for all sources in Scan 008 on 980609n. J-band uncertainties are shown in blue, H-band in green and K_s in red.

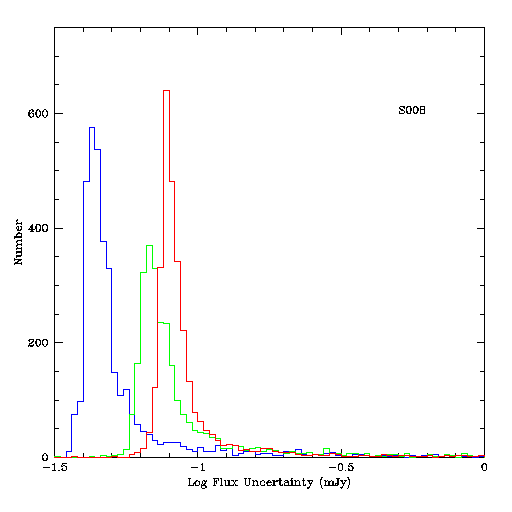
Figure 5 - Histogram of PROPHOT flux uncertainties for all sources in Scan 022 on 980627s. J-band uncertainties are shown in blue, H-band in green and K_s in red.

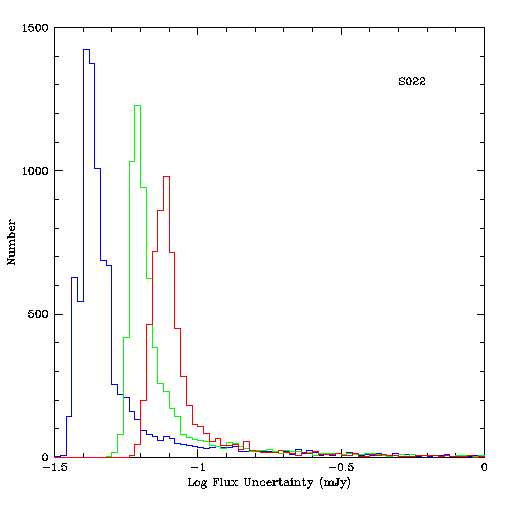
Figure 6 - Histogram of PROPHOT flux uncertainties for all sources in Scan 051 on 980627s. J-band uncertainties are shown in blue, H-band in green and K_s in red.

The Point Source Noise Response to Source Density, Background and Seeing

To be a useful noise estimator for the purpose of thresholding sources for catalog generation, the point source noise should respond to confusion noise due to source crowding, as well as other factors which affect sensitivity such as sky background levels and seeing. To investigate this, I have evaluated the characteristic point source noise from 1,186 photometric scans taken on the 19 northern and southern nights currently available on-line for production processing. The point source noise for each scan was measured by forming the histogram of the logarithm of the flux uncertainties quoted by PROPHOT for all R2-R1 sources not identified with artifacts (as in figures 4-7), and estimating the mode of the error distributions by selecting the peak bin of the histograms. The bin size of the histograms was 0.015 in log mJy, so there is some binning uncertainty, and in the event that two peaks were detected in the histograms, the lower noise peak was always selected.

a. Source Density

Figure 7 shows the points source estimates for all scans in the 19 nights, plotted as a function of the total number of detections in the respective bands. Data from the northern scans are shown in black and from southern scans in red. The J-band noise is shown in the top panel, H in the center and K_s at the bottom.

Figure 7 - Point Source Noise Estimate as a Function of Total Number of Sources in a Scan (black = northern data, red = southern data)

The total number of detections in a scan is not a robust estimate of true source density (and therefore confusion noise) because the point source detections algorithm automatically adjusts to higher flux levels in response to higher source density. This is illustrated in figures 8-10 which show the differential source counts for each band in the the three sample scans discussed above. The completeness level, as gauged by the multi-band turnover point (multi-bandedness is a very good reliability indicator) in each curve is nearly 2 magnitudes brighter in scan 051 compared with scans 008 and 022.

Figure 8 - Differential source counts for Scan 008 on 980609n. J-counts are shown in blue, H in green, and K_s in red. Counts for single band sources are shown as solid lines, and multi-band counts are shown as dashed lines.

Figure 9 - Differential source counts for Scan 022 on 980627s. J-counts are shown in blue, H in green, and K_s in red. Counts for single band sources are shown as solid lines, and multi-band counts are shown as dashed lines.

Figure 10 - Differential source counts for Scan 051 on 980627s. J-counts are shown in blue, H in green, and K_s in red. Counts for single band sources are shown as solid lines, and multi-band counts are shown as dashed lines.

Figure 11 shows the point source noise estimate for each scan plotted as a function of the total number of non-artifact detections brighter than 13th magnitude in each band. This fiducial point was chosen because it remains relatively complete in dense fields (it must be somewhat incomplete, of course, particularly in K_s) yet still has enough sources in low density scans to provide a useful comparison. The distributions show that the point source noise is clearly elevated in the densest scans, but remain relatively unaffected for densities up to nearly 10⁴ sources per scan in the K_s band. Although the relationship between the point source noise and density should be probed further with some scans that fill out the density range sampled by these data, it is clear that this noise estimator does respond to increasing source density.

Figure 11 - Point Source Noise Estimate as a Function of Number of M<13 Sources in a Scan(black = northern data, red = southern data)

b. Sky Background

Figure 12 - Point Source Noise Estimate as a Function of Mean Background Level in a Scan (black = northern data, red = southern data)

c. Seeing

Figure 13 - Point Source Noise Estimate as a Function of Mean Seeing Shape in a Scan (black = northern data, red = southern data)

d. Point Source Photometric Sensitivity Parameter (PSP)

The relationship between achieved point source photometric sensitivity and the sky background and seeing has been investigated empirically using the repeatability of photometry using the six-scan calibration sets. The achieved SNR=10:1 (observed RMS=0.108 mags) level was found to be proportional to a simple function of the mean seeing shape (SH) and the mean frame background (BG). This function, called the Photometric Sensitivity Parameter, scales as SH*BG^+0.29. Figure 14 shows the point source noise estimates plotted as a function of the Photometric Sensitivity Parameter for the sample scans, and there is a very clean dependence in the estimator on this empirical sensitivity parameter.

Figure 14 - Point Source Noise Estimate as a Function of Photometric Sensitivity Parameter (SH * BG^0.29) (black = northern data, red = southern data)

The comparison between the point source noise estimator and the Photometric Sensitivity Parameter allows us to get some feeling for the meaning of this point source noise. For example, the analysis of achieved photometric repeatability indicated that a scan had a 50% probability of meeting the Level 1 Requirements for photometric sensitivity at H and K_s for PSP values ~11.1. Figure 14 indicates that for K_s, this corresponds to a noise level of approximately 0.1 mJy. Thus, the SNR=10:1 level would occur for sources with point source flux densities of ~1mJy, which is essentially the Level 1 Sensitivity Requirement. For the H-band, extrapolation of the the northern data to PSP values of 11.1 indicates a point source noise of ~0.08 mJy. The southern data points extrapolate to a slightly higher noise than the northern data, ~0.1 mJy (note that the PSP was defined using northern data only, and has not yet been normalized for the south). Again, this suggests effective SNR=10:1 levels around ~1mJy which is essentially the Level 1 Photometric Sensitivity Requirement.

Given the tight relationship between the point source noise and the PSP, one might be tempted to use the PSP to estimate the effective noise level in a scan, and threshold using that noise. Unfortunately, this is not viable because the PSP does not include any correction for source density. The islands of scans at high noise levels seen in figure 14 are the high density scans.

It should be emphasized that the point source noise estimator discussed here provides a scan-average noise. For scans in which the seeing and/or background vary rapidly, the characteristic noise level may be inaccurate for portions of the scan. However, such scans usually suffer from other problems such as residual background structure due to severe airglow or PSF-mismatches, so this error in the noise evaluation is not the most severe problem.

Effective Signal-To-Noise Thresholds for Catalog Generation

As a reference point, the maximum J, H and K_s scan point source noise values from the 2MASS Sampler night, 971116n, are 0.046, 0.077 and 0.075 mJy, respectively. The equivalent SNR=6:1 levels for these noise levels are 16.47, 15.91 and 15.48 magnitudes. The magnitude thresholds used to construct the Sampler point source catalog were 16.5, 16.0 and 15.5 magnitudes at J, H and K_s for multi-band sources. These thresholds were established after extensive visual review of sources overlayed on images, as well as examination of the completeness levels inferred from the repeatiability of the photometry in the calibration scan sets.