IRAS Explanatory Supplement
V. Data Reduction
C. Source Detection
Table of Contents | Index | Previous Section | Next Section
The calibrated raw data for each of the 59 operating detectors were examined for point sources and small extended sources. The detection of the latter is described in Section V.E.1. For each observation the accepted point source detections were passed, with detector number, time of detection (and uncertainty), flux (and uncertainty), signal-to-noise ratio (SNR), and the correlation coefficient with the point source template (CC, see below), to the seconds-confirmation processor (Section V.D.2). A noise history was also created for each detector. If a detection occurred in a one-second period in which the analog-to-digital converter was saturated, then the detection was flagged.
C.1 Square Wave Filter

|
|
Figure V.C.1 a) An eight-point zero-sum,
square-wave filter was applied to the data streams (top panel);
b) The detection processor looked for positive square wave peaks
between zero crossings in the filtered data stream (bottom panel). larger largest |
The first step in the detection process was to search for potential sources by applying a narrow bandpass digital filter to the detector data streams. This filter consisted of an eight-point zero-sum square-wave function. The effect of the filter was to subtract the first two and last two points from the sum of the middle four points; more formally, for a sequence of data points xi (Fig. V.C.1a), the amplitude of the square-wave of x at the point i is defined as:
(V.C.1)
This square-wave filter was applied at each point in the data stream,
and a search was made for positive square-wave excursions between zero
crossings, defined as a pair of data points (i,j) such that
(see Fig. V.C.1b):
|
E(x,i) > 0; E(x,k) >/- 0 for i </- k </- j; E(x,j+1) < 0; and for some n, E(x,n) < 0 and E(x,n),....., E(x,i-1) < 0. |
 p
p
 j, such that E(x,p)
is maximal among
E(x,i),..., E(x,j). Peaks with
square-wave amplitudes, E(n,p), greater than 2.5
times the noise Nx were passed on as candidates
for point sources.
j, such that E(x,p)
is maximal among
E(x,i),..., E(x,j). Peaks with
square-wave amplitudes, E(n,p), greater than 2.5
times the noise Nx were passed on as candidates
for point sources.
C.2 Noise Estimator
The noise Nx for a data stream was defined as the median of all E(x,p) for square-wave peaks p. Such positive square-wave excursions occurred about once every 6 samples. It was found from prelaunch simulations and from analysis of in-flight data that this median noise estimator gave a reasonable representation of the rms noise, in the sense that
(V.C.2)
The initial value of Nx was the median of the first
50 square-wave peaks. Nx was then updated at every
square-wave peak E(x,p) as follows:
The parameter
The noise estimate was maintained in a noise history file for each detector
after multiplication by the factor to convert it to an estimate of the
rms noise on a single sample. To compress the size of this file, an entry
was made only if linear extrapolation of the previous two entries would
lead to an error greater than 35%.
The time of the square-wave peak at E(x,p) was estimated
from the maximum of the parabola passing through the three points (p
- 1,E(x,p - 1)), (p,E(x,p)), (p + 1,
E(x,p + 1)). The delay between a source in the unfiltered data
and its peak in the square-wave function was subtracted from the estimate to
give the detection time. A small offset to account for electronic delay and
the sampling time of the detector was included. The timing uncertainty was
taken from a look-up
table as a function of the values of signal-to-noise ratio and correlation
coefficient for the source.
The heart of the point source detection processor was the comparison
of the data for candidate sources selected by the square-wave filter with
the profile, or template, expected for an ideal point source. For this
purpose the 11 samples centered on the candidate detection time,
Yi, i = 0...10, were compared with the appropriately
shifted template Ri superimposed on a linear baseline. The
amplitude A of the detection was determined from fitting the 11 data values
Yi to the function
(V.C.3) (V.C.3.2) (V.C.3.3)
(V.C.4.1)
The correlation coefficient of yi with
Ri is given by
(V.C.5)
where (V.C.5.1) A candidate detection was accepted only if
(i) (V.C.6.1) (ii) (V.C.6.2)
where the factor 1.2 converts the median noise estimate to an rms noise
estimate (see Section V.C.2).
The total rms uncertainty in amplitude, A, over the 11 data samples
can be shown to be
(V.C.7)
Thus the correlation coefficient is a measure of the local signal-to-noise
ratio and a threshold of 0.87 corresponds to a signal-to-noise ratio of
about 5.7. In regions where the noise was roughly independent of time,
the main thresholding was therefore provided by the correlation coefficient.
The square-wave filter threshold (Section V.C.1 above)
was set low so that
as few acceptable detections as possible were rejected, within the constraints
of the available computer time. It should be noted that a low correlation
coefficient for a bright point-source is probably an indication that the
source is slightly extended. In regions of high source density
(see Section V.H.6),
where extended structure is a considerable problem, the correlation
coefficient threshold was increased to 0.97.
The templates for each wavelength band were stored with a sampling
frequency 64 times that of the survey data. The candidate detection time in
sampling was determined, rounded off to the nearest 1/64th of a sample and
the appropriate 11-point template selected by taking every 64th point from
the template array.
Immediately after launch, predicted detector responses to an ideal point
source were used. Composite templates were constructed for each detector
using sources detected with high correlation coefficient and signal-to-noise
ratio. The a priori templates were replaced with the composite templates
and the analysis repeated, using 12 hours worth of data. Convergence was
achieved after only a few iterations. Figure V.C.2
shows representative
point source templates for one detector in each wavelength band. Since
no evidence for detector-to-detector variation within a band was found,
the results for all the detectors in each band were averaged together to
produce the final composite templates.
A secondary class of detections called low signal-to-noise detections
was defined as those with signal-to-noise ratios between 3 and the threshold
required for a valid detection. Because the threshold for valid detections
was itself set at 3, no low signal-to-noise detections should have been
generated. However, due to the round-off errors in the computation of the
signal-to-noise ratio, a few were created. These were only used to provide
upper limits for sources confirmed in other bands.
When two sources crossed the same detector within 6 samples of each
other, i.e., within 1.4', 1.4', 2.9', 5.9' of each other in the scan direction
at 12, 25, 60 and 100 µm, respectively, the detection of one
or both of the sources may have been inhibited. Generally, the brighter
source was detected without mishap, but the fainter source may have had
its baseline so modified by the brighter source that it failed to be detected
at all. This is the phenomenon of source "shadowing". A source
may have been shadowed in a longer wavelength band but detected perfectly
at shorter wavelengths. To warn of the possibility of this effect, sources
were tagged at a later stage in the processing
(see Section V.H.3) If they
had near neighbors. The fluxes of such flagged sources should be regarded
with caution. No significance should be attached to the absence of a detected
flux in a shadowed band. The completeness figures given in
Chapter VIII
do not apply to the shadow zone around a source.
 rms
rms
 1.2 Nx
1.2 Nx
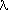 (< 1); otherwise, increase Nx by the factor
1/
(< 1); otherwise, increase Nx by the factor
1/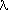 .
.
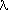 controlled the stability
of the noise estimator. As
controlled the stability
of the noise estimator. As 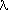 approached 1,
the noise estimator became very stable, but it also lagged behind any change
in the noise by about 5/(1 -
approached 1,
the noise estimator became very stable, but it also lagged behind any change
in the noise by about 5/(1 - 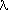 )
samples. In tuning the value of
)
samples. In tuning the value of 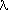 great
importance was attached to achieving a stable noise estimate at high Galactic
latitudes, where the noise was mainly due to detector noise, and a value
great
importance was attached to achieving a stable noise estimate at high Galactic
latitudes, where the noise was mainly due to detector noise, and a value
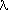 = 0.95 was set at 12, 25 and 60 µm,
and 0.90 at 100 µm. This meant that the noise estimate lagged by about
25', 25', 50', 50' at
12, 25, 60 and 100 µm. Regions with steep gradients in the density
of point sources, such as the Galactic plane, had large gradients in the
noise amplitude. Hence the noise was underestimated as the plane was
approached and overestimated after it was passed
(Sections V.C.7,
VIII.D.6). This error was very large, and
since sources were thresholded partly on signal-to-noise ratio
(Section V.C.4, below), the effective threshold was raised
to very large values after passing the Galactic plane, resulting in a shadow
zone in which few sources were accepted. To keep the extent of the 100
µm shadow zone no larger than that at 60 µm,
= 0.95 was set at 12, 25 and 60 µm,
and 0.90 at 100 µm. This meant that the noise estimate lagged by about
25', 25', 50', 50' at
12, 25, 60 and 100 µm. Regions with steep gradients in the density
of point sources, such as the Galactic plane, had large gradients in the
noise amplitude. Hence the noise was underestimated as the plane was
approached and overestimated after it was passed
(Sections V.C.7,
VIII.D.6). This error was very large, and
since sources were thresholded partly on signal-to-noise ratio
(Section V.C.4, below), the effective threshold was raised
to very large values after passing the Galactic plane, resulting in a shadow
zone in which few sources were accepted. To keep the extent of the 100
µm shadow zone no larger than that at 60 µm,
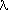 was set to 0.90 at 100 µm compared
with 0.95 at 60 µm. However, this
adversely affected the stability of the 100 µm noise estimate
in the presence of cirrus at higher Galactic latitudes, resulting in the
rejection of some detections that should have been accepted and hence a
reduction in completeness of the catalog at 100 µm
(Section VIII.D).
was set to 0.90 at 100 µm compared
with 0.95 at 60 µm. However, this
adversely affected the stability of the 100 µm noise estimate
in the presence of cirrus at higher Galactic latitudes, resulting in the
rejection of some detections that should have been accepted and hence a
reduction in completeness of the catalog at 100 µm
(Section VIII.D).
C.3 Timing Estimate
C.4 Correlation with Point Source Template


 stands for
stands for








 ,
,

C.5 Determination of Templates

Figure V.C.2 Detections found by the square-wave filter
were compared with the response of the telescope-detector-electronics
combination to a true point source. Representative point source
templates are shown for one detector in each wavelength band.
larger
largest
C.6 Low Signal-to-Noise Detections
C.7 Source Shadowing
Table of Contents |
Index |
Previous Section
| Next Section