The Swiss Cheese Algorithm
- Author:
- Serge Monkewitz
| Contents | |
Definitions and Terms
- D1 : Apparition
Let
 be the complete set of observed apparitions
be the complete set of observed apparitions  . The total number of apparitions
. The total number of apparitions  is equal to
is equal to 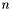 .
. - D2 : Position
Each apparition
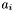 has a position on the sky
has a position on the sky  , specified as a unit vector in
, specified as a unit vector in 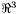 (that is,
(that is,  ).
). - D3 : Distance
Define the distance between two positions
 to be
to be ![\[ d(v_1, v_2) = \arccos{(v_1 \cdot v_2)} \]](form_127.png)
- D4 : Match set
Given
 , define the radius-R match set for
, define the radius-R match set for 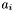 as follows :
as follows : ![\[ M_R(i) = \{ a_j |\: a_j \in A,\: j \neq i,\: d(p_i, p_j) \leq R \} \]](form_129.png)
- D5 : Apparition (group) centroid
Each apparition
 has a centroid
has a centroid  which is defined as follows :
which is defined as follows : ![\[ v = p_i + \sum p_j \:,\; a_j \in M_\phi(i) \]](form_131.png)
![\[ v_i = \frac{v}{\Vert v \Vert} \]](form_132.png)
where
 will be referred to as the density radius.
will be referred to as the density radius. - D6 : Apparition density
Each apparition
 has an integer density
has an integer density  :
: ![\[ \rho_i = 2^{42}(|M_{\phi}(i)| + 1) + 2^{21}(|M_{0.66\phi}(i)| + 1) + |M_{0.33\phi}(i)| + 1 \]](form_135.png)
- D7 : Group
A group is a set of nearby apparitions likely to be obvservations of the same astronomical source. Define the group
 to be the set of apparitions within the group radius
to be the set of apparitions within the group radius  of the apparition centroid
of the apparition centroid  :
: ![\[ G_s = \{ a_j |\: a_j \in A,\: d(v_s,p_j) \leq \theta \} \]](form_139.png)
Note that the group radius
 should be set so that if
should be set so that if  for two apparitions
for two apparitions 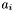 and
and  , then they are very unlikely to be observations of the same astronomical source.
, then they are very unlikely to be observations of the same astronomical source. - D8 : Confused apparition
A confused apparition is an apparition that belongs to more than one group.
- D9 : Confused group
A confused group is a group that contains at least one confused apparition.
- D10 : Group count
Each apparition
 has a group count
has a group count  which is equal to the number of groups
which is equal to the number of groups 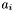 has been assigned to. Note that:
has been assigned to. Note that: -
 is confused
is confused -
 is unconfused
is unconfused -
 does not belong to any groups
does not belong to any groups
 .
. -
- D11 : Group type
Each group
 has a group type
has a group type  which takes the following values :
which takes the following values : -
 : signifies that
: signifies that  is unconfused, and was generated by a swiss cheese pass.
is unconfused, and was generated by a swiss cheese pass. -
 : signifies that
: signifies that  is unconfused, and was generated by a cheese crumbling pass.
is unconfused, and was generated by a cheese crumbling pass. -
 : signifies that
: signifies that  is confused, and was generated by a swiss cheese pass.
is confused, and was generated by a swiss cheese pass. -
 : signifies that
: signifies that  is confused, and was generated by a cheese crumbling pass.
is confused, and was generated by a cheese crumbling pass.
-
- D12 : Seed set
The seed set is the set of apparitions which are to be considered as the starting points for generating groups.
- D13 : Seed flag
Each apparition
 has a seed flag
has a seed flag 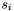 which takes the following values :
which takes the following values : -
 : signifies that the apparition has been removed from the set of seeds by a cheese crumbling pass.
: signifies that the apparition has been removed from the set of seeds by a cheese crumbling pass. -
 : signifies that the apparition is not in the set of seeds.
: signifies that the apparition is not in the set of seeds. -
 : signifies that the apparition is to be considered as the starting point for a group by swiss cheese passes.
: signifies that the apparition is to be considered as the starting point for a group by swiss cheese passes. -
 : signifies that the apparition is to be considered as the starting point for a group by cheese crumbling passes.
: signifies that the apparition is to be considered as the starting point for a group by cheese crumbling passes.
-
- D14 : Group counter
Each generated group has an integer group counter that uniquely identifies it within the set of all generated groups.
- D15 : Apparition counter
Each apparition
 has an integer apparition counter
has an integer apparition counter  which uniquely identifies
which uniquely identifies 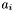 in
in  .
. - D16 : Apparition comparison
The operators
 ,
,  ,
,  for apparitions are defined as follows :
for apparitions are defined as follows : -

-

-
 either
either  or
or 
-
- D17 : Apparition scan key
Each apparition optionally has a scan key which identifies the scan it was extracted from.
- D18 : Scan count
Each group has a scan count, equal to the number of scans containing at least one apparition belonging to the group.
- D19 : Apparition count
Each group has an apparition count, equal to the number of apparitions belonging to the group.
Algorithm Input and Output
The WAX application currently retrieves apparitions from a single database table, and stores results in up to 3 database tables. The DBMS hosting the input and output tables is required to support ESQL/C (WAX is currently capable of communicating only with the Informix RDBMS).Input Apparition Table
WAX assumes that the apparition table contains columns corresponding to a 32-bit integer unique identifier (see D16), as well as J2000 right ascension and declination (handled internally as double precision floating point values). If coverage computation is desired, WAX can optionally retrieve scan keys which correspond to 32-bit integer unique identifiers for the scans apparitions were extracted from. If left unspecified, these columns are assumed to be namedcntr, ra, dec, and scan_key. Additional retrieval columns can be specified at compile time - for more information concerning this feature, please see the Writing WAX Plug-Ins documentation page. Group Information Table
This output table contains group attributes. The following columns will be present for each generated group :-
gcntr: the group counter, a unique identifier for the group -
napp: the group apparition count -
gtype: the group type -
sdet(optional) : the group scan count
Group-apparition Link Table
This output table contains links between groups and apparitions. The following columns will be present for each distinct group-apparition pair :-
gcntr: the group counter, a unique identifier for the group -
cntr: the apparition counter, a unique identifier for the apparition -
ngrp: the group count, the number of groups the apparition belongs to
Singleton Table
Normally, single apparition groups (singletons) are stored in the group information table. However, if the end-user of the WAX application so desires, WAX can store singletons in a seperate table.
This output table will normally contain a single column named gcntr, a unique identifier for the single apparition group (see D14). This is the only column necessary since all singletons have an apparition count and scan count equal to 1, and a group type of 0. Note that when a singleton table is in use, singletons are not recorded in the link table since singletons always have group counters equal to their apparition counters.
Finally, there is a compile time option to include all columns retrieved from the input table in the singleton table (just as for the group-apparition link table). For more details, see the Usage Examples documentation section of the srcgen (Source Code Generator) helper application.
Grouped Apparition Table
This optional table contains information pertaining to grouped apparitions, calculated during the output pass of the swiss cheese algorithm, and allows (via the plug-in interface) a "best" group to be picked for a given apparition.
This output table will normally contain a single column named cntr, a unique identifier for the grouped apparition (see D15).
Basic Algorithm
The swiss cheese algorithm is conceptually simple, and consists of the following steps :-
Set

-
Compute

-
Using the comparison operators defined for apparitions in D16, renumber (sort) the apparitions
 such that given any two distinct
such that given any two distinct  where
where  , then the condition
, then the condition  holds if and only if
holds if and only if  .
. -
Now, generate groups as follows :
-
Find the apparition
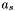 with
with  such that
such that  where
where  and
and  .
. -
Find
 and
and  , increment
, increment  and set
and set  .
. -
If
 with
with  , continue at step 1. Otherwise, the algorithm has completed.
, continue at step 1. Otherwise, the algorithm has completed.
-
Find the apparition
In practice, the algorithm as described would be very hard to implement since the size of  can be much greater than the physical memory available to a computer. It is therefore necessary to limit processing to small subsets of
can be much greater than the physical memory available to a computer. It is therefore necessary to limit processing to small subsets of  . Because the computation of groups and apparition centroids involves finding apparitions in the immediate vicinity of positions on the sky, it is natural to split
. Because the computation of groups and apparition centroids involves finding apparitions in the immediate vicinity of positions on the sky, it is natural to split  into subsets corresponding to apparitions from distinct regions of the sky. A simple way of doing this is to partition the sky into a sequence of annuli (or bands) which each cover a range of declinations.
into subsets corresponding to apparitions from distinct regions of the sky. A simple way of doing this is to partition the sky into a sequence of annuli (or bands) which each cover a range of declinations.
The Parallel Swiss Cheese Algorithm
Sky Subdivision: Dec Bands
Consider the set of subsets of ,
,  where
where  is a dec band containing all apparitions with positions falling into the declination range
is a dec band containing all apparitions with positions falling into the declination range  . The bands are numbered such that
. The bands are numbered such that  . Furthermore,
. Furthermore,  degrees and
degrees and  degrees (for a small positive constant
degrees (for a small positive constant  ). Clearly, the union of the bands is equal to
). Clearly, the union of the bands is equal to  , and band
, and band  is adjacent to bands
is adjacent to bands  and
and  .
.
A particular band  is fully processed when every group stemming from a centroid with declination falling into the range
is fully processed when every group stemming from a centroid with declination falling into the range  has been generated (and those with centroids in
has been generated (and those with centroids in  have been stored). For each apparition
have been stored). For each apparition  belonging to such a group, all groups containing
belonging to such a group, all groups containing  must have been generated so that the group count for
must have been generated so that the group count for  is valid prior to storage.
is valid prior to storage.
Consider the group  generated around the centroid
generated around the centroid  . The seed apparition for the group,
. The seed apparition for the group, 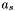 , is within distance
, is within distance  of
of  . Therefore, if every apparition in the declination range
. Therefore, if every apparition in the declination range  has been removed from the set of seeds, then all groups with centroids inside
has been removed from the set of seeds, then all groups with centroids inside  will have been generated.
will have been generated.
Now consider an apparition  . All groups containing
. All groups containing 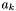 will have been generated when
will have been generated when  and there exists no apparition
and there exists no apparition  with
with  and
and  . Note that for such an apparition to exist,
. Note that for such an apparition to exist,  .
.
Therefore, if  with
with  in the declination range
in the declination range  , then
, then  has been fully processed. Groups generated from apparitions in that declination range will include apparitions in the range
has been fully processed. Groups generated from apparitions in that declination range will include apparitions in the range  , and, in order to compute densities and centroids for them, the declination range
, and, in order to compute densities and centroids for them, the declination range  must be considered. For simplicity we consider only the maximum density radius,
must be considered. For simplicity we consider only the maximum density radius,  , arriving at the conclusion that in order to fully process the band
, arriving at the conclusion that in order to fully process the band  , it is necessary to consider apparitions inside the declination range
, it is necessary to consider apparitions inside the declination range  . This condition, looser than strictly necessary, is not sufficient. To see why, reconsider the Basic Algorithm. It is clearly possible for an apparition
. This condition, looser than strictly necessary, is not sufficient. To see why, reconsider the Basic Algorithm. It is clearly possible for an apparition  not in the declination range
not in the declination range  to be denser than all apparitions in
to be denser than all apparitions in  . Furthermore, generating
. Furthermore, generating  could potentially remove apparitions inside the dec band from the set of seeds. Without considering
could potentially remove apparitions inside the dec band from the set of seeds. Without considering  , it would therefore be impossible to finish processing
, it would therefore be impossible to finish processing  . In the general case,
. In the general case,  must be considered in its entirety to fully process
must be considered in its entirety to fully process  .
.
If this situation is encountered, the parallel swiss cheese algorithm changes the optimal order (as defined by the Basic Algorithm) in which apparitions are considered for grouping.
Primary and Secondary Bands
- Primary Band
A primary band
 is a band where
is a band where  is even.
is even. - Secondary Band
A secondary band
 is a band where
is a band where  is odd.
is odd.
For band  , the apparitions in the declination range
, the apparitions in the declination range  where
where  are considered (currently,
are considered (currently,  is set to
is set to 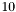 by default). If the condition
by default). If the condition  is enforced, then the regions on the sky being considered by any two non-adjacent bands are disjoint. In particular, no two primary or secondary bands will process regions that overlap. Therefore all primary bands can be processed independently and in parallel. Secondary bands can also be processed independently of eachother and in parallel, but do depend on the results of adjacent primary bands.
is enforced, then the regions on the sky being considered by any two non-adjacent bands are disjoint. In particular, no two primary or secondary bands will process regions that overlap. Therefore all primary bands can be processed independently and in parallel. Secondary bands can also be processed independently of eachother and in parallel, but do depend on the results of adjacent primary bands.
By forcing primary bands to save any information which effects adjacent secondary bands, it is possible to guarantee full processing of secondary bands with a significantly tighter declination range.
A primary band  will store a list of groups generated around centroids with declination greater than or equal to
will store a list of groups generated around centroids with declination greater than or equal to  (the top group list for
(the top group list for  ), and a list of groups generated around centroids with declination less than
), and a list of groups generated around centroids with declination less than  (the bottom group list for
(the bottom group list for  ). The groups in these lists will be stored according to the order in which they were generated.
). The groups in these lists will be stored according to the order in which they were generated.
Furthermore, group counts for apparitions in the declination range  (the top apparition set for
(the top apparition set for  ) as well as group counts for apparitions in
) as well as group counts for apparitions in  (the bottom apparition set for
(the bottom apparition set for  ) will be stored.
) will be stored.
Before creating any new groups, a secondary band  will read the top group list and apparition set generated by
will read the top group list and apparition set generated by  as well as the bottom group list and apparition set generated by
as well as the bottom group list and apparition set generated by  and generate the indicated groups in the given order. Essentially, the secondary band will blindly copy the work of its neighbours. This behaviour gives each primary band the latitude to deviate from the group generation order imposed by the Basic Algorithm.
and generate the indicated groups in the given order. Essentially, the secondary band will blindly copy the work of its neighbours. This behaviour gives each primary band the latitude to deviate from the group generation order imposed by the Basic Algorithm.
What follows is a detailed description of the various steps of the swiss cheese algorithm.
Step 1: Apparition Retrieval
Consider the band to be processed,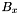 . If
. If 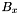 is a primary band, all apparitions in the declination range
is a primary band, all apparitions in the declination range  are retrieved. Otherwise all apparitions in
are retrieved. Otherwise all apparitions in  are retrieved.
are retrieved.
Define the removal flag  for apparition
for apparition 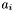 as follows :
as follows :
-
 doesn't have to be removed from the set of seeds to finish processing
doesn't have to be removed from the set of seeds to finish processing 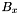 .
. -
 must be removed from the set of seeds to finish processing
must be removed from the set of seeds to finish processing 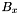 .
.
Finally, define the total seed count  to equal the sum of the removal flags of all retrieved apparitions.
to equal the sum of the removal flags of all retrieved apparitions.
Now for each retrieved apparition, set  . Also set
. Also set  .
.
Step 2: Density Pass
If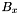 is a primary band the following steps are performed for each apparition
is a primary band the following steps are performed for each apparition 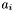 in the declination range
in the declination range  :
: -
find

-
compute
 from
from 
-
compute
 from
from 
-
if
 is in
is in  , set
, set  , otherwise set
, otherwise set  .
. -
if
 is in
is in  , set
, set  and increment
and increment  .
.
Otherwise, for each apparition 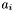 in
in  :
:
-
find

-
compute
 from
from 
-
compute
 from
from 
-
if
 is in
is in  , set
, set  , otherwise set
, otherwise set  .
. -
if
 is in
is in  , set
, set  and increment
and increment  .
.
Step 3: Stitching Pass (Secondary Bands Only)
This pass simply reads the top apparition set and group list generated by band as well as the bottom apparition set and group list generated by band
as well as the bottom apparition set and group list generated by band  . Each apparition listed in the apparition sets has its group count set to the saved value, after which the saved groups are generated in the indicated order.
. Each apparition listed in the apparition sets has its group count set to the saved value, after which the saved groups are generated in the indicated order. Step 4: Swiss Cheese Pass
Step 4.1
Examine the next as yet unconsidered apparition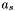 with
with  , find the match set
, find the match set  and continue to step 4.2. Note that the order in which apparitions are considered is unimportant (this means that apparitions can be considered in spatial order, allowing match sets to be found efficiently).
and continue to step 4.2. Note that the order in which apparitions are considered is unimportant (this means that apparitions can be considered in spatial order, allowing match sets to be found efficiently).
If there is no such 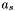 , then the pass has completed. At this point, if the pass did not generate any new groups and
, then the pass has completed. At this point, if the pass did not generate any new groups and  , the algorithm has reached an impasse and continues with a Cheese Crumbling Pass.
, the algorithm has reached an impasse and continues with a Cheese Crumbling Pass.
If  , then
, then 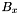 has been completely processed and the algorithm continues with the Output Pass.
has been completely processed and the algorithm continues with the Output Pass.
Otherwise, another swiss cheese pass is performed.
Step 4.2
At this point the region around as must be examined, keeping in mind that groups should be generated based on a sequence of apparitions ordered by decreasing density.
Now, a group must be generated from 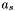 if there is no other apparition
if there is no other apparition 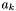 with
with  (a seed) that is "denser" than
(a seed) that is "denser" than 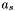 (
( ) which might generate a group containing
) which might generate a group containing 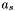 .
.
Any group containing 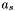 must have a centroid within distance
must have a centroid within distance  of
of 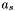 , that is to say, must be generated from an apparition within distance
, that is to say, must be generated from an apparition within distance  of
of 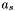 .
.
So, if  with
with  and
and  , then continue at step 4.3.
, then continue at step 4.3.
Otherwise continue at step 4.1.
Step 4.3
Scan the set of apparitions to find
to find  . Now set
. Now set  and subtract
and subtract 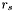 from
from  . Next,
. Next,  with
with  , set
, set  and subtract
and subtract  from
from  . Finally, set the group type of
. Finally, set the group type of  to
to 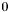 and continue with step 4.4.
and continue with step 4.4. Step 4.4
If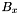 is a primary band :
is a primary band : -
if
 has declination greater than or equal to
has declination greater than or equal to  , append
, append  to the top group list.
to the top group list. -
if
 has declination less than
has declination less than  , append
, append  to the bottom group list.
to the bottom group list. -
Increment the group count for every apparition in

Otherwise :
-
Increment the group count for every apparition in
 that falls inside the declination range
that falls inside the declination range  .
.
Finally, if  is inside
is inside  :
:
-
Set the group counter for
 to
to 
-
If requested, compute the group scan count by sorting the apparitions in
 on scan key and then counting the number of unique scan key values
on scan key and then counting the number of unique scan key values - Store a record of the generated group in memory
Step 5: Cheese Crumbling Pass (Primary Bands Only)
This pass is identical to the swiss cheese pass, except for the following: only apparitions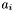 with
with  are considered as starting points for group generation. Furthermore, seed apparitions from which groups are generated have their seed flag values set to
are considered as starting points for group generation. Furthermore, seed apparitions from which groups are generated have their seed flag values set to  (not
(not 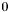 ).
). Step 6: Output Pass
If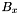 is a primary band :
is a primary band : - Save the top group list, bottom group list, top apparition set, and bottom apparition set to disk.
For each group  stored by step 4.4 :
stored by step 4.4 :
-
Scan the apparitions in
 . If any of them has a group count greater than
. If any of them has a group count greater than 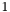 , add
, add  to
to  (marking the group confused). Also find the z-component
(marking the group confused). Also find the z-component 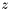 of the seed apparition's centroid (this is the apparition with counter equal to the group counter for
of the seed apparition's centroid (this is the apparition with counter equal to the group counter for  ).
). -
Pass
 to a pluggable group parameter computation stage which computes group attributes (such as an average position, average magnitudes, etc...).
to a pluggable group parameter computation stage which computes group attributes (such as an average position, average magnitudes, etc...). -
Lastly, if
 , insert
, insert  and its associated apparitions and attributes into the various database output tables.
and its associated apparitions and attributes into the various database output tables.
For each apparition  in
in  , pass the list of groups containing
, pass the list of groups containing  to a pluggable apparition parameter computation stage which computes attributes for
to a pluggable apparition parameter computation stage which computes attributes for  . Finally, insert
. Finally, insert  and its associated attributes into the grouped apparition table.
and its associated attributes into the grouped apparition table.
Generated on Thu Oct 21 13:19:39 2004 for WAX Version 2.1 by